Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn cách giải bài 3 trang 133 trong sách bài tập Toán 11 - Chân trời sáng tạo tập 1.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách cẩn thận, kèm theo các bước giải thích rõ ràng, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và M là trung điểm của SA. Tìm giao tuyến của mặt phẳng (P) với các mặt của hình chóp S. ABCD, biết rằng (P) đi qua M, song song với SC và AD.
Đề bài
Cho hình chóp S. ABCD có đáy ABCD là hình bình hànhvà M là trung điểm của SA. Tìm giao tuyến của mặt phẳng (P) với các mặt của hình chóp S. ABCD, biết rằng (P) đi qua M, song song với SC và AD.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để tìm giao tuyến: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).
+ Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để tìm giao tuyến: Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Lời giải chi tiết
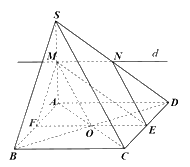
Gọi O là giao điểm AC và BD, E là trung điểm của CD.
Vì M, O lần lượt là trung điểm của SA, AC nên MO là đường trung bình của tam giác SAC, suy ra SC//MO. Mà \(MO \subset \left( {MOE} \right)\), SC không nằm trong mặt phẳng (MOE) nên SC//(MOE) (1).
Vì E, O lần lượt là trung điểm của CD, AC nên EO là đường trung bình của tam giác DAC, suy ra AD//EO. Mà \(EO \subset \left( {MOE} \right)\), AD không nằm trong mặt phẳng (MOE) nên AD//(MOE) (2).
Từ (1) và (2) suy ra: Mặt phẳng (P) là mặt phẳng (MOE).
Trong mặt phẳng (ABCD), gọi F là giao điểm của OE và AB.
Mà \(OE \subset \left( {MOE} \right),AB \subset \left( {ABCD} \right)\) nên \(\left( {MOE} \right) \cap \left( {ABCD} \right) = EF,\left( {MOE} \right) \cap \left( {ABS} \right) = FM\)
Vì \(M \in \left( {MOE} \right) \cap \left( {SAD} \right),OE//AD\) nên giao tuyến của mặt phẳng (MOE) và mặt phẳng (SAD) là đường thẳng d qua M song song với AD, OE.
Trong mặt phẳng (SAD), gọi N là giao điểm của d và SD.
Do đó, \(\left( {MOE} \right) \cap \left( {SAD} \right) = MN,\left( {MOE} \right) \cap \left( {SCD} \right) = EN\)
Bài 3 trang 133 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc hai. Để giải bài này, học sinh cần nắm vững kiến thức về:
Nội dung bài 3: Bài 3 thường yêu cầu học sinh xác định các yếu tố của hàm số bậc hai (a, b, c), tìm đỉnh, trục đối xứng, giao điểm với các trục tọa độ, vẽ đồ thị hàm số và khảo sát sự biến thiên của hàm số.
Để giải bài 3 trang 133 hiệu quả, bạn cần:
(Ở đây sẽ là lời giải chi tiết cho bài 3 trang 133, bao gồm các bước giải, giải thích rõ ràng và các ví dụ minh họa. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.)
Ví dụ, nếu bài 3 yêu cầu tìm đỉnh của parabol y = x2 - 4x + 3, lời giải sẽ như sau:
Hàm số y = x2 - 4x + 3 có dạng y = ax2 + bx + c, với a = 1, b = -4, c = 3.
Hoành độ đỉnh của parabol là x0 = -b / (2a) = -(-4) / (2 * 1) = 2.
Tung độ đỉnh của parabol là y0 = f(x0) = f(2) = 22 - 4 * 2 + 3 = -1.
Vậy, đỉnh của parabol là (2, -1).
Ngoài bài 3 trang 133, còn rất nhiều bài tập tương tự về hàm số bậc hai. Dưới đây là một số dạng bài tập thường gặp và cách giải:
Để học tốt môn Toán 11, đặc biệt là phần hàm số bậc hai, bạn nên:
Bài 3 trang 133 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng rằng, với lời giải chi tiết và các hướng dẫn trong bài viết này, bạn sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!
| Công thức | Mô tả |
|---|---|
| x0 = -b / (2a) | Hoành độ đỉnh của parabol |
| y0 = f(x0) | Tung độ đỉnh của parabol |