Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 3 trang 55 sách bài tập Toán 11 Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài giải chi tiết dưới đây!
Cho tứ diện ABCD có \(DA \bot \left( {ABC} \right)\), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ \(AH \bot MD\) tại H.
Đề bài
Cho tứ diện ABCD có \(DA \bot \left( {ABC} \right)\), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ \(AH \bot MD\) tại H.
a) Chứng minh rằng \(AH \bot \left( {BCD} \right)\).
b) Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Chứng minh rằng \(GK \bot \left( {ABC} \right)\).
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về định lí đường thẳng vuông góc với mặt phẳng để chứng minh: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
b) Sử dụng kiến thức về liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng: Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Lời giải chi tiết
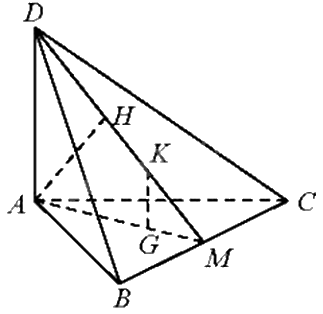
a) Vì \(DA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow DA \bot BC\)
Tam giác ABC cân tại A nên AM là đường trung tuyến đồng thời là đường cao, suy ra: \(BC \bot AM\)
Vì \(DA \bot BC\), \(BC \bot AM\), DA và AM cắt nhau tại A và nằm trong (DAM) nên \(BC \bot \left( {DAM} \right)\). Lại có, \(AH \subset \left( {DAM} \right) \Rightarrow AH \bot BC\)
Ta có: \(AH \bot MD\), \(AH \bot BC\), MD và BC cắt nhau tại M và nằm trong (BCD) nên \(AH \bot \left( {BCD} \right)\)
b) Tam giác DBC có K là trọng tâm và DM là đường trung tuyến nên \(\frac{{DK}}{{DM}} = \frac{2}{3}\)
Tam giác ABC có G là trọng tâm và AM là đường trung tuyến nên \(\frac{{AG}}{{AM}} = \frac{2}{3}\)
Tam giác ADM có: \(\frac{{DK}}{{DM}} = \frac{{AG}}{{AM}}\left( { = \frac{2}{3}} \right)\) nên KG//AD (định lí Thalès đảo)
Mà \(DA \bot \left( {ABC} \right)\) nên \(GK \bot \left( {ABC} \right)\).
Bài 3 trang 55 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết, từng bước, giúp các em hiểu rõ cách tiếp cận và giải quyết bài toán này.
Bài 3 yêu cầu tính đạo hàm của các hàm số sau:
Áp dụng công thức đạo hàm của tổng và hiệu, ta có:
y' = (x3)' - (3x2)' + (2x)' - (5)'
y' = 3x2 - 6x + 2
Áp dụng công thức đạo hàm của tích, ta có:
y' = (x2 + 1)'(x - 2) + (x2 + 1)(x - 2)'
y' = 2x(x - 2) + (x2 + 1)(1)
y' = 2x2 - 4x + x2 + 1
y' = 3x2 - 4x + 1
Áp dụng công thức đạo hàm của thương, ta có:
y' = [(2x + 1)'(x - 3) - (2x + 1)(x - 3)'] / (x - 3)2
y' = [2(x - 3) - (2x + 1)(1)] / (x - 3)2
y' = (2x - 6 - 2x - 1) / (x - 3)2
y' = -7 / (x - 3)2
Áp dụng công thức đạo hàm của hàm lượng giác, ta có:
y' = (sin(2x))' + (cos(x))'
y' = cos(2x) * 2 - sin(x)
y' = 2cos(2x) - sin(x)
Khi tính đạo hàm, cần nắm vững các công thức đạo hàm cơ bản của các hàm số đơn giản. Ngoài ra, cần chú ý áp dụng đúng các công thức đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Bài 3 trang 55 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp các em rèn luyện kỹ năng tính đạo hàm. Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin hơn khi giải các bài tập tương tự. Chúc các em học tập tốt!
| Hàm số | Đạo hàm |
|---|---|
| y = x3 - 3x2 + 2x - 5 | y' = 3x2 - 6x + 2 |
| y = (x2 + 1)(x - 2) | y' = 3x2 - 4x + 1 |
| y = (2x + 1) / (x - 3) | y' = -7 / (x - 3)2 |
| y = sin(2x) + cos(x) | y' = 2cos(2x) - sin(x) |