Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 3 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi và luyện tập để nắm vững kiến thức Toán 11 nhé!
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’. Tính khoảng cách giữa hai đường thẳng MN và B’D’.
Đề bài
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’. Tính khoảng cách giữa hai đường thẳng MN và B’D’.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khoảng cách giữa hai đường thẳng chéo nhau để tính: Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó, kí hiệu d(a, b).
Lời giải chi tiết
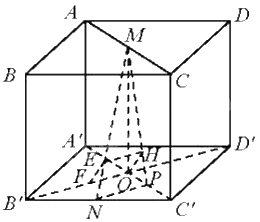
Gọi O là giao điểm của B’D’ và A’C’. Gọi P là trung điểm của OC’.
Vẽ \(OH \bot MP,HE//NP,EF//OH\) (H thuộc MP, E thuộc MN, F thuộc B’D’)
Chứng minh được \(B'D' \bot \left( {A'C'CA} \right)\) nên \(B'D' \bot OH\), mà \(EF//OH\) nên \(EF \bot B'D'\left( 1 \right)\)
Vì NP//B’D’ nên \(NP \bot \left( {A'C'CA} \right) \Rightarrow NP \bot OH\), mà \(OH \bot MP\) nên \(OH \bot \left( {MNP} \right)\) hay \(OH \bot MN\), mà \(EF//OH\)\( \Rightarrow EF \bot MN\left( 2 \right)\)
Từ (1) và (2) ta có: \(d\left( {MN,B'D'} \right) = EF = OH\)
Tam giác MOP vuông tại O, ta có: \(OM = a,OP = \frac{1}{2}OC' = \frac{1}{4}A'C' = \frac{{a\sqrt 2 }}{4}\) nên
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{P^2}}} + \frac{1}{{O{M^2}}} = {\left( {\frac{4}{{a\sqrt 2 }}} \right)^2} + \frac{1}{{{a^2}}} = \frac{9}{{{a^2}}}\)\( \Rightarrow OH = \frac{a}{3}\)
Bài 3 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về phép biến hình. Bài tập này yêu cầu học sinh vận dụng kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán thực tế. Việc nắm vững các tính chất và công thức liên quan đến các phép biến hình là vô cùng quan trọng để hoàn thành tốt bài tập này.
Bài 3 bao gồm các câu hỏi và bài tập khác nhau, tập trung vào việc xác định ảnh của một điểm, một đường thẳng hoặc một hình qua các phép biến hình. Cụ thể, bài tập yêu cầu:
Để giải quyết bài 3 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2, học sinh cần:
Ví dụ 1: Cho điểm M(2, -3) và vectơ v = (1, 2). Tìm ảnh M' của M qua phép tịnh tiến theo vectơ v.
Giải:
Áp dụng công thức phép tịnh tiến: M'(x', y') = M(x, y) + v(a, b) = (x + a, y + b)
Ta có: x' = 2 + 1 = 3 và y' = -3 + 2 = -1
Vậy M'(3, -1).
Khi giải bài tập về phép biến hình, cần chú ý đến các yếu tố sau:
Để củng cố kiến thức và kỹ năng giải bài tập về phép biến hình, các em có thể tự giải các bài tập sau:
Bài 3 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu sâu về các phép biến hình. Bằng cách nắm vững kiến thức, phương pháp giải và luyện tập thường xuyên, các em sẽ tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán 11.
| Phép biến hình | Công thức biến đổi tọa độ |
|---|---|
| Tịnh tiến | M'(x', y') = M(x, y) + v(a, b) = (x + a, y + b) |
| Quay | M'(x', y') = Q(O, α)(M(x, y)) |
| Đối xứng trục | M'(x', y') = Đd(M(x, y)) |
| Đối xứng tâm | M'(x', y') = ĐI(M(x, y)) |