Bài 4 trang 128 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh tính đạo hàm, tìm cực trị, và vẽ đồ thị hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 128 sách bài tập Toán 11 Chân trời sáng tạo tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và M, N lần lượt là trung điểm của AB, CD. (P) là mặt phẳng đi qua MN và song song với mặt phẳng (SAD). Tìm giao tuyến của các mặt hình chóp với mặt phẳng (P).
Đề bài
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và M, N lần lượt là trung điểm của AB, CD. (P) là mặt phẳng đi qua MN và song song với mặt phẳng (SAD). Tìm giao tuyến của các mặt hình chóp với mặt phẳng (P).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng (Q) thì (P) song song với (Q).
Lời giải chi tiết
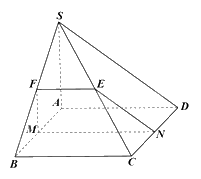
Vì M, N lần lượt là trung điểm của AB, CD nên MN//BC//AD
Mà \(AD \subset \left( {SAD} \right)\), MN không nằm trong (SAD) nên MN//(SAD)
Gọi E là trung điểm của SC.
Vì N, E lần lượt là trung điểm của CD, SC nên NE là đường trung bình của tam giác SCD, suy ra NE//SD.
Mà \(SD \subset \left( {SAD} \right)\), NE không nằm trong mặt phẳng (SAD) nên NE//(SAD).
Vì MN//(SAD), NE//(SAD), NE và MN cắt nhau tại N và nằm trong mặt phẳng (MNE) nên (MNE)//(SAD).
Gọi F là trung điểm của SB, tương tự ta có (MNEF) là mặt phẳng (P).
Vậy \(\left( P \right) \cap \left( {ABCD} \right) = MN\) với MN//BC//AD.
\(\left( P \right) \cap \left( {SAB} \right) = MF\) với MF//SA (F là trung điểm của SB)
\(\left( P \right) \cap \left( {SCD} \right) = NE\) với NE//SD (E là trung điểm của SC)
\(\left( P \right) \cap \left( {SCB} \right) = FE\)
Bài 4 trang 128 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
(Giả sử đề bài là: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.)
y' = 3x2 - 6x
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2.
Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.
Ngoài bài 4 trang 128, sách bài tập Toán 11 Chân trời sáng tạo tập 1 còn nhiều bài tập tương tự về đạo hàm và ứng dụng của đạo hàm. Để giải các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Khi giải bài tập về đạo hàm, học sinh cần lưu ý những điều sau:
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, và bài tập về Toán 11. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em nắm vững kiến thức và đạt kết quả cao trong học tập.