Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 3 trang 51 sách bài tập Toán 11 Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài giải chi tiết dưới đây!
Cho tứ diện ABCD có \(AB = CD,AC = BD,AD = BC\). a) Chứng minh đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc hai cạnh đó.
Đề bài
Cho tứ diện ABCD có \(AB = CD,AC = BD,AD = BC\).
a) Chứng minh đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc hai cạnh đó.
b) Chứng minh hai đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc với nhau.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về hai đường thẳng vuông góc trong không gian để chứng minh.
Lời giải chi tiết
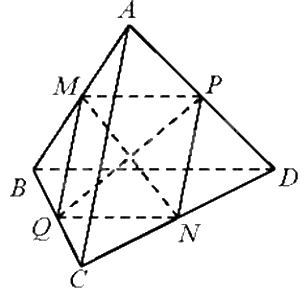
a) Gọi M, N, P, Q lần lượt là trung điểm của AB, CD, AD, BC.
Tam giác ADC và tam giác BCD có: CD chung, \(AC = BD,AD = BC\)
Suy ra, \(\Delta ADC = \Delta BCD\left( {c.c.c} \right)\) nên \(AN = BN\) (hai đường trung tuyến ứng với cạnh CD)
Do đó, tam giác NAB cân tại N. Do đó, NM là đường trung tuyến đồng thời là đường cao. Do đó, \(NM \bot AB\)
Chứng minh tương tự ta có: \(NM \bot CD\)
Vậy đoạn nối các trung điểm của các cặp cạnh đối thì vuông góc hai cạnh đó
b) Vì MQ là đường trung bình của tam giác ABC nên \(MQ = \frac{{AC}}{2}\)
Vì PN là đường trung bình của tam giác ADC nên \(PN = \frac{{AC}}{2}\). Do đó, \(MQ = PN = \frac{{AC}}{2}\)
Chứng minh tương tự ta có: \(MP = QN = \frac{{BD}}{2}\)
Mà \(AC = BD\). Do đó, \(MQ = PN = MP = QN\)
Suy ra, tứ giác MPNQ là hình thoi, suy ra \(MN \bot PQ\)
Bài 3 trang 51 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về hàm số bậc hai. Để giải bài này, học sinh cần nắm vững kiến thức về định nghĩa hàm số, tập xác định, tập giá trị, và các tính chất của hàm số bậc hai.
Bài 3 yêu cầu học sinh xác định tập xác định của hàm số. Để làm được điều này, cần lưu ý các điều kiện sau:
Để minh họa, ta xét một số ví dụ cụ thể:
Khi gặp bài tập về tập xác định, học sinh nên thực hiện theo các bước sau:
Trong quá trình giải bài tập, cần chú ý các điểm sau:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Bài 3 trang 51 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh hiểu rõ hơn về tập xác định của hàm số. Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng trên đây, các em sẽ tự tin hơn trong quá trình học tập và làm bài tập.
| Hàm số | Tập xác định |
|---|---|
| y = √(x - 2) | D = [2; +∞) |
| y = 1/(x + 1) | D = R \ {-1} |
| y = log₂(x - 3) | D = (3; +∞) |