Bài 2 trang 51 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân. Bài tập này thường yêu cầu học sinh vận dụng các công thức và tính chất đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 trang 51 sách bài tập Toán 11 Chân trời sáng tạo tập 2, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \(SA = a\sqrt 3 ,SA \bot AC,\) \(SA \bot BC,\) \(\widehat {BAD} = {120^0}\).
Đề bài
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \(SA = a\sqrt 3 ,SA \bot AC,\) \(SA \bot BC,\) \(\widehat {BAD} = {120^0}\). Gọi M, N lần lượt là trung điểm của AD, BC. Tính góc giữa các cặp đường thẳng:
a) SD và BC.
b) MN và SC.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về góc giữa hai đường thẳng trong không gian để tính: Góc giữa hai đường thẳng a, b trong không gian, kí hiệu (a, b), là góc giữa hai đường thẳng \(a'\) và \(b'\) cùng đi qua một điểm và lần lượt song song hoặc trùng với a và b.
Góc giữa hai đường thẳng nhận giá trị từ \({0^0}\) đến \({90^0}\).
Lời giải chi tiết
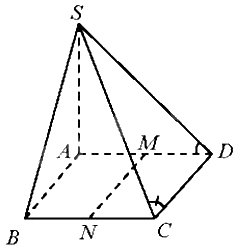
a) Vì ABCD là hình thoi nên AD//BC. Do đó, \(\left( {SD,BC} \right) = \left( {SD,AD} \right) = \widehat {SDA}\)
Vì \(SA \bot BC,\) AD//BC nên \(SA \bot AD\). Do đó, tam giác SAD vuông tại A.
Do đó, \(\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \Rightarrow \widehat {SDA} = {60^0}\)
b) Vì M, N lần lượt là trung điểm của AD, BC nên MN//CD
Do đó, \(\left( {MN,SC} \right) = \left( {CD,SC} \right) = \widehat {SCD}\)
Áp dụng định lí Pythagore vào tam giác SAD vuông tại A có: \(SD = \sqrt {S{A^2} + A{D^2}} = \sqrt {3{a^2} + {a^2}} = 2a\)
Vì ABCD là hình thoi nên \(AD = DC\). Do đó, tam giác ACD cân tại D
Vì ABCD là hình thoi nên AC là tia phân giác góc BAD. Do đó, \(\widehat {DAC} = \frac{1}{2}\widehat {BAD} = {60^0}\)
Suy ra, tam giác ACD đều nên \(AC = a\)
Áp dụng định lí Pythagore vào tam giác SAC vuông tại A có: \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {3{a^2} + {a^2}} = 2a\)
Áp dụng định lý cosin vào tam giác SCD có:
\(\cos \widehat {SCD} = \frac{{S{C^2} + C{D^2} - S{D^2}}}{{2.SC.CD}} = \frac{{{{\left( {2a} \right)}^2} + {a^2} - {{\left( {2a} \right)}^2}}}{{2.2a.a}} = \frac{1}{4} \Rightarrow \widehat {SCD} \approx 75,{5^0}\)
Bài 2 trong sách bài tập Toán 11 Chân trời sáng tạo tập 2 tập trung vào việc ứng dụng các kiến thức về dãy số, đặc biệt là cấp số cộng và cấp số nhân, vào giải quyết các bài toán thực tế. Nội dung bài tập thường xoay quanh việc xác định số hạng tổng quát, tính tổng của dãy số, và tìm các yếu tố liên quan đến cấp số cộng/nhân.
Để giải quyết bài 2 trang 51 một cách hiệu quả, học sinh cần nắm vững các bước sau:
(Giả sử đề bài là: Cho dãy số (un) với u1 = 2 và un+1 = 2un - 1. Tìm số hạng thứ 5 của dãy.)
Giải:
Vậy số hạng thứ 5 của dãy là 17.
Ngoài bài 2 trang 51, học sinh có thể gặp các dạng bài tập tương tự như:
Để luyện tập hiệu quả, học sinh nên:
Khi giải bài tập về dãy số, học sinh cần lưu ý:
Bài 2 trang 51 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về dãy số. Bằng cách nắm vững các kiến thức cơ bản và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.