Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 4 trang 61 sách bài tập Toán 11 Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các bạn. Hãy cùng theo dõi và luyện tập để nắm vững kiến thức Toán 11 nhé!
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD).
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi H và K lần lượt là hình chiếu của A trên SB và SD. Chứng minh rằng:
a) \(\left( {SBC} \right) \bot \left( {SAB} \right)\);
b) \(\left( {SCD} \right) \bot \left( {SAD} \right)\);
c) \(\left( {SBD} \right) \bot \left( {SAC} \right)\);
d) \(\left( {SAC} \right) \bot \left( {AHK} \right)\).
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về điều kiện để hai mặt phẳng vuông góc: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
+ Sử dụng kiến thức về tính chất cơ bản của hai mặt phẳng vuông góc: Nếu hai mặt phẳng cắt nhau cùng vuông góc với nhau mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.
d) Sử dụng kiến thức về tính chất cơ bản của hai mặt phẳng vuông góc: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.
Lời giải chi tiết
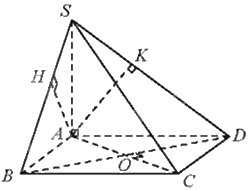
Vì hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD), và SA là giao tuyến của hai mặt phẳng (SAB) và (SAD) nên \(SA \bot \left( {ABCD} \right)\)
a) Vì ABCD là hình vuông nên \(AB \bot BC\).
Mà \(SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC\)
Do đó, \(BC \bot \left( {SAB} \right)\). Lại có: \(BC \subset \left( {SBC} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\)
b) Vì ABCD là hình vuông nên \(AD \bot DC\).
Mà \(SA \bot \left( {ABCD} \right),DC \subset \left( {ABCD} \right) \Rightarrow SA \bot DC\)
Do đó, \(DC \bot \left( {SAD} \right)\). Lại có: \(DC \subset \left( {SDC} \right) \Rightarrow \left( {SCD} \right) \bot \left( {SAD} \right)\)
c) Vì ABCD là hình vuông nên \(AC \bot DB\).
Mà \(SA \bot \left( {ABCD} \right),DB \subset \left( {ABCD} \right) \Rightarrow SA \bot DB\)
Do đó, \(DB \bot \left( {SAC} \right)\). Lại có: \(DB \subset \left( {SDB} \right) \Rightarrow \left( {SBD} \right) \bot \left( {SAC} \right)\)
d) Vì \(\left( {SBC} \right) \bot \left( {SAB} \right)\), SB là giao tuyến của (SBC) và (SAB), \(AH \bot SB\) nên \(HA \bot \left( {SBC} \right) \Rightarrow AH \bot SC\)
Vì \(\left( {SCD} \right) \bot \left( {SAD} \right)\), SD là giao tuyến của (SDC) và (SAD), \(AK \bot SD\) nên \(KA \bot \left( {SDC} \right) \Rightarrow AK \bot SC\)
Do đó, \(SC \bot \left( {AHK} \right)\). Mà \(SC \subset \left( {SAC} \right) \Rightarrow \left( {SAC} \right) \bot \left( {AHK} \right)\)
Bài 4 trang 61 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về phép biến hình. Bài tập này yêu cầu học sinh vận dụng kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán thực tế. Việc nắm vững các tính chất và công thức liên quan đến các phép biến hình là yếu tố then chốt để hoàn thành bài tập này một cách hiệu quả.
Bài 4 bao gồm các dạng bài tập sau:
Để giải quyết dạng bài này, học sinh cần nắm vững công thức biến đổi tọa độ của điểm qua từng phép biến hình:
Ví dụ: Cho điểm M(2, 3) và vectơ v = (1, -2). Tìm tọa độ điểm M' là ảnh của M qua phép tịnh tiến theo vectơ v.
Giải: M'(2 + 1, 3 - 2) = M'(3, 1).
Để tìm tâm của phép biến hình, học sinh cần sử dụng các công thức và tính chất liên quan. Ví dụ, tâm của phép tịnh tiến là điểm sao cho vectơ tịnh tiến bằng vectơ nối giữa điểm gốc và điểm ảnh.
Để chứng minh một phép biến hình là phép biến hình nào đó, học sinh cần kiểm tra xem phép biến hình đó có thỏa mãn các tính chất của phép biến hình đó hay không.
Trong các bài toán hình học, phép biến hình có thể được sử dụng để chuyển đổi một hình về một hình tương đương, giúp đơn giản hóa việc chứng minh hoặc tính toán.
Để củng cố kiến thức, các bạn có thể tự giải thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Việc luyện tập thường xuyên sẽ giúp các bạn nắm vững kiến thức và tự tin hơn khi làm bài thi.
Bài 4 trang 61 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng, giúp học sinh rèn luyện kỹ năng vận dụng kiến thức về phép biến hình vào giải quyết các bài toán thực tế. Hy vọng với hướng dẫn chi tiết này, các bạn sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán 11.