Bài 5 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về hàm số và đồ thị hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Hãy cùng theo dõi lời giải chi tiết dưới đây để hiểu rõ hơn về cách giải bài tập này nhé!
Cho hàm số \(y = \tan x\) với \(x \in \left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) \cup \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\). a) Vẽ đồ thị của hàm số đã cho.
Đề bài
Cho hàm số \(y = \tan x\) với \(x \in \left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) \cup \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
a) Vẽ đồ thị của hàm số đã cho.
b) Tìm các giá trị của \(x \in \left[ { - \frac{{7\pi }}{4};\frac{\pi }{4}} \right]\) sao cho \(\sqrt 3 \tan \left( {x + \frac{\pi }{4}} \right) + 1 = 0\).
c) Tìm các giá trị của \(x \in \left[ { - \frac{{5\pi }}{6};\frac{\pi }{6}} \right]\) sao cho \(\tan \left( {2x + \frac{\pi }{6}} \right) \ge - \frac{{\sqrt 3 }}{3}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về đồ thị hàm số \(y = \tan x\) để giải.
Lời giải chi tiết
a) Ta có đồ thị của hàm số \(y = \tan x\) với \(x \in \left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) \cup \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\):
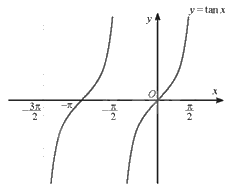
b) \(\sqrt 3 \tan \left( {x + \frac{\pi }{4}} \right) + 1 = 0\) khi \(\tan \left( {x + \frac{\pi }{4}} \right) = \frac{{ - \sqrt 3 }}{3}\)
Đặt \(x + \frac{\pi }{4} = t\). Vì \(\frac{{ - 7\pi }}{4} \le x \le \frac{\pi }{4} \Rightarrow \frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\)
Hàm số \(y = \tan t\) xác định khi \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\). Kết hợp với điều kiện \(\frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\) ta có \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\).
Đồ thị hàm số \(y = \tan t\) với \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\) là:
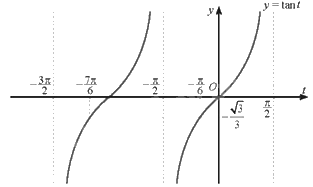
Từ đồ thị hàm số trên ta có:
\(\tan t = \frac{{ - \sqrt 3 }}{3}\) khi và chỉ khi \(t = \frac{{ - 7\pi }}{6}\) hoặc \(t = \frac{{ - \pi }}{6}\).
Suy ra: \(x + \frac{\pi }{4} = \frac{{ - 7\pi }}{6}\) hoặc \(x + \frac{\pi }{4} = \frac{{ - \pi }}{6}\). Do đó, \(x = \frac{{ - 17\pi }}{{12}}\) hoặc \(x = \frac{{ - 5\pi }}{{12}}\).
c) Đặt \(2x + \frac{\pi }{6} = t\). Vì \(\frac{{ - 5\pi }}{6} \le x \le \frac{\pi }{6} \Rightarrow \frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\)
Hàm số \(y = \tan t\) xác định khi \(t \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\). Kết hợp với điều kiện \(\frac{{ - 3\pi }}{2} \le t \le \frac{\pi }{2}\) ta có \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\)
Đồ thị hàm số \(y = \tan t\) với \(t \in \left( {\frac{{ - 3\pi }}{2};\frac{{ - \pi }}{2}} \right) \cup \left( {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right)\) là:
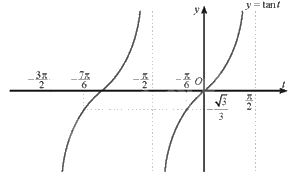
Từ đồ thị hàm số trên ta có:
\(\tan t \ge \frac{{ - \sqrt 3 }}{3}\) khi và chỉ khi \(\frac{{ - 7\pi }}{6} \le t < - \frac{\pi }{2}\) hoặc \(\frac{{ - \pi }}{6} \le t < \frac{\pi }{2}\).
Suy ra, \(\frac{{ - 7\pi }}{6} \le 2x + \frac{\pi }{6} < - \frac{\pi }{2}\) hoặc \(\frac{{ - \pi }}{6} \le 2x + \frac{\pi }{6} < \frac{\pi }{2}\)
Do đó, \(\frac{{ - 2\pi }}{3} \le x < - \frac{\pi }{3}\) hoặc \( - \frac{\pi }{6} \le x < \frac{\pi }{6}\).
Bài 5 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Đề bài yêu cầu chúng ta xác định các yếu tố của parabol và vẽ đồ thị hàm số. Phương pháp giải bài tập này bao gồm các bước sau:
(Giả sử đề bài là: Xác định các yếu tố của parabol y = x2 - 4x + 3 và vẽ đồ thị.)
Bước 1: Xác định hệ số a, b, c
Hàm số y = x2 - 4x + 3 có a = 1, b = -4, c = 3.
Bước 2: Tính tọa độ đỉnh của parabol
xđỉnh = -(-4)/(2*1) = 2
yđỉnh = -( (-4)2 - 4*1*3 )/(4*1) = -(16 - 12)/4 = -1
Vậy, tọa độ đỉnh của parabol là I(2; -1).
Bước 3: Xác định trục đối xứng của parabol
Trục đối xứng của parabol là x = 2.
Bước 4: Xác định giao điểm của parabol với trục Oy
Giao điểm của parabol với trục Oy là A(0; 3).
Bước 5: Xác định giao điểm của parabol với trục Ox
Giải phương trình x2 - 4x + 3 = 0
Δ = (-4)2 - 4*1*3 = 16 - 12 = 4
x1 = (4 + √4)/(2*1) = 3
x2 = (4 - √4)/(2*1) = 1
Vậy, giao điểm của parabol với trục Ox là B(1; 0) và C(3; 0).
Bước 6: Vẽ đồ thị hàm số
Dựa vào các yếu tố đã xác định, ta có thể vẽ đồ thị hàm số y = x2 - 4x + 3.
Khi giải bài tập về hàm số bậc hai, học sinh cần chú ý các điểm sau:
Hàm số bậc hai có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài 5 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Chúc các em học tập tốt!