Bài 2 trang 149 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về kiến thức đã học. Bài tập này thường yêu cầu vận dụng các công thức, định lý đã được trình bày trong sách giáo khoa để giải quyết các vấn đề cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 trang 149, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Một kĩ thuật viên ghi lại cân nặng của 20 chi tiết máy ở bảng sau (đơn vị: gam) a) Tính cân nặng trung bình của mỗi chi tiết máy. b) Lập bảng tần số ghép nhóm của mẫu số liệu trên với nhóm đầu tiên là \(\left[ {5,40;5,45} \right)\) và ước lượng số trung bình của mẫu số liệu ghép nhóm trên.
Đề bài
Một kĩ thuật viên ghi lại cân nặng của 20 chi tiết máy ở bảng sau (đơn vị: gam)

a) Tính cân nặng trung bình của mỗi chi tiết máy.
b) Lập bảng tần số ghép nhóm của mẫu số liệu trên với nhóm đầu tiên là \(\left[ {5,40;5,45} \right)\) và ước lượng số trung bình của mẫu số liệu ghép nhóm trên.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về số trung bình của mẫu số liệu để tính:
Giả sử mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm:
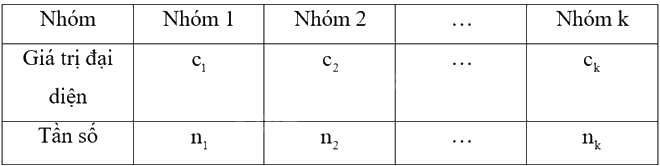
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).
Lời giải chi tiết
a) Cân nặng trung bình của mỗi chi máy là:
\((5,63 + 5,58 + 5,42 + 5,58 + 5,56 + 5,54 + 5,55 + 5,40 + 5,60 + 5,56 + 5,46\)
\( + 5,51 + 5,58 + 5,48 + 5,61 + 5,50 + 5,54 + 5,64 + 5,43 + 5,63):20 = 5,54{\rm{ }}\left( g \right)\)
b) Ta hiệu chỉnh bảng tần số ghép nhóm bao gồm các giá trị đại diện của nhóm là:
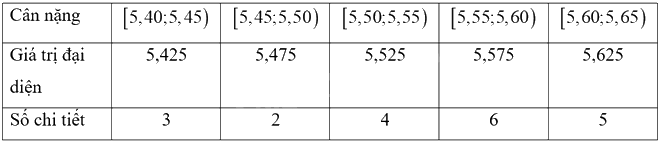
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline x = \frac{{5,425.3 + 5,475.2 + 5,525.4 + 5,575.6 + 5,625.5}}{{3 + 2 + 4 + 6 + 5}} = 5,545\left( g \right)\)
Bài 2 trang 149 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc tính đạo hàm của hàm số, tìm điểm cực trị, và khảo sát hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài 2 trang 149. Giả sử bài 2 yêu cầu tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1.
Giải:
Để tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1, ta sử dụng các quy tắc tính đạo hàm:
Áp dụng các quy tắc trên, ta có:
f'(x) = 3x2 - 6x + 2
Vậy, đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1 là f'(x) = 3x2 - 6x + 2.
Để hiểu rõ hơn về cách tính đạo hàm, chúng ta cùng xem xét một số ví dụ minh họa:
Ngoài ra, các bạn có thể tự giải các bài tập tương tự để rèn luyện kỹ năng:
Khi giải bài tập về đạo hàm, các bạn cần lưu ý một số điểm sau:
Bài 2 trang 149 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các kiến thức cơ bản và áp dụng các quy tắc tính đạo hàm một cách chính xác, các bạn có thể giải bài tập này một cách dễ dàng và hiệu quả. Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và các ví dụ minh họa trên sẽ giúp các bạn học tập tốt hơn.