Bài 4 trang 133 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh tính đạo hàm, tìm cực trị, và vẽ đồ thị hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 133, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a và tam giác SAB đều. Gọi M là điểm thuộc cạnh BC sao cho \(BM = x\left( {0 < x < a} \right)\), mặt phẳng \(\left( \alpha \right)\) đi qua M song song với hai đường thẳng SA và AB. a) Xác định giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp. b) Tính diện tích hình tạo bởi các đoạn giao tuyến ở câu a theo a và x.
Đề bài
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a và tam giác SAB đều. Gọi M là điểm thuộc cạnh BC sao cho \(BM = x\left( {0 < x < a} \right)\), mặt phẳng \(\left( \alpha \right)\) đi qua M song song với hai đường thẳng SA và AB.
a) Xác định giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp.
b) Tính diện tích hình tạo bởi các đoạn giao tuyến ở câu a theo a và x.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để tìm giao tuyến: Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Lời giải chi tiết
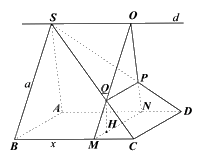
a) Trong mặt phẳng (ABCD), kẻ MN//AB//CD (N thuộc AD)
Trong mặt phẳng (SAD), kẻ đường thẳng d đi qua S và song song với AD. Qua N kẻ đường thẳng song song với SA cắt d tại O.
Gọi P là giao điểm của NO và SD, Q là giao điểm của MO và SC.
Khi đó, \(\left( \alpha \right)\) là mặt phẳng (OMN).
Ta có:
\(\left( \alpha \right) \cap \left( {ABCD} \right) = MN,\left( \alpha \right) \cap \left( {SBC} \right) = MQ,\left( \alpha \right) \cap \left( {SCD} \right) = PQ,\left( \alpha \right) \cap \left( {ASD} \right) = PN.\)
b) Các giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp tạo thành tứ giác MNPQ.
Vì CD//MN//PQ nên tứ giác MNPQ là hình thang với \(MN = AB = a,\widehat {QMN} = \widehat {SBA} = {60^0}\)
Trong tam giác SBC có MQ//SB nên theo hệ quả định lí Thalès ta có: \(\frac{{MQ}}{{SB}} = \frac{{MC}}{{BC}}\)
Mà \(SB = BC \Rightarrow MQ = MC = a - x\)
Trong tam giác SDC có PQ//CD nên theo hệ quả định lí Thalès ta có: \(\frac{{PQ}}{{CD}} = \frac{{SQ}}{{SC}}\)
Trong tam giác SBC có MQ//SB nên theo định lí Thalès ta có: \(\frac{{SQ}}{{SC}} = \frac{{MB}}{{BC}}\)
Do đó, \(\frac{{PQ}}{{CD}} = \frac{{BM}}{{BC}}\), mà \(CD = BC \Rightarrow QP = BM = x\)
Qua Q kẻ đường thẳng vuông góc với MN cắt MN tại H.
Ta có: \(\widehat {SBA} = \widehat {HMQ} = {60^0}\)
Khi đó, \(QH = MQ.\sin \widehat {QMH} = MQ.\sin {60^0} = \frac{{\left( {a - x} \right)\sqrt 3 }}{2}\)
Vậy diện tích hình thang MNPQ là: \(S = \frac{1}{2}QH\left( {MN + PQ} \right) = \frac{1}{2}.\frac{{\left( {a - x} \right)\sqrt 3 }}{2}\left( {a + x} \right) = \frac{{\left( {{a^2} - {x^2}} \right)\sqrt 3 }}{4}\) (đvdt)
Bài 4 trong sách bài tập Toán 11 Chân trời sáng tạo tập 1 tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến sự biến thiên của hàm số. Cụ thể, bài toán yêu cầu học sinh phân tích hàm số, tìm điểm cực trị, và xác định khoảng đồng biến, nghịch biến của hàm số. Việc nắm vững các khái niệm và kỹ năng này là nền tảng quan trọng để học tốt các chương trình Toán học nâng cao hơn.
Trước khi đi vào giải chi tiết, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và lựa chọn phương pháp giải phù hợp. Thông thường, để giải bài 4 trang 133, học sinh cần thực hiện các bước sau:
Để minh họa, chúng ta sẽ cùng nhau giải một ví dụ cụ thể. Giả sử hàm số được cho là y = x3 - 3x2 + 2.
y' = 3x2 - 6x
Giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Hàm số y = x3 - 3x2 + 2 có điểm cực đại tại x = 0, với giá trị y = 2, và điểm cực tiểu tại x = 2, với giá trị y = -2.
Ngoài bài 4 trang 133, sách bài tập Toán 11 Chân trời sáng tạo tập 1 còn nhiều bài tập tương tự khác. Để giải quyết các bài tập này, học sinh cần nắm vững các kiến thức và kỹ năng sau:
Để học tốt môn Toán 11, đặc biệt là phần đạo hàm, học sinh nên:
Bài 4 trang 133 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Bằng cách phân tích đề bài, lựa chọn phương pháp giải phù hợp, và luyện tập thường xuyên, học sinh có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán 11.