Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 12 trang 77 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp cho bạn các bước giải bài tập một cách rõ ràng, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất cho học sinh, sinh viên. Hãy cùng theo dõi bài viết này để hiểu rõ hơn về cách giải bài tập và áp dụng vào các bài tập tương tự nhé!
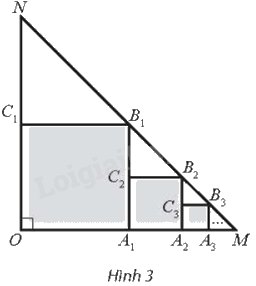
Cho tam giác OMN vuông cân tại O, \(OM = ON = 1\). Trong tam giác OMN, vẽ hình vuông \(O{A_1}{B_1}{C_1}\) sao cho các đỉnh \({A_1},{B_1},{C_1}\) lần lượt nằm trên các cạnh OM, MN, ON. Trong tam giác \({A_1}M{B_1}\), vẽ hình vuông \({A_1}{A_2}{B_2}{C_2}\) sao cho các đỉnh \({A_2},{B_2},{C_2}\) lần lượt nằm trên các cạnh \({A_1}M,M{B_1},{A_1}{B_1}\). Tiếp tục quá trình đó, ta được một dãy các hình vuông (Hình 3). Tính tổng diện tích các hình vuông này.
Đề bài
Cho tam giác OMN vuông cân tại O, \(OM = ON = 1\). Trong tam giác OMN, vẽ hình vuông \(O{A_1}{B_1}{C_1}\) sao cho các đỉnh \({A_1},{B_1},{C_1}\) lần lượt nằm trên các cạnh OM, MN, ON. Trong tam giác \({A_1}M{B_1}\), vẽ hình vuông \({A_1}{A_2}{B_2}{C_2}\) sao cho các đỉnh \({A_2},{B_2},{C_2}\) lần lượt nằm trên các cạnh \({A_1}M,M{B_1},{A_1}{B_1}\). Tiếp tục quá trình đó, ta được một dãy các hình vuông (Hình 3). Tính tổng diện tích các hình vuông này.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tổng của cấp số nhân lùi vô hạn để tính tổng: Cấp số nhân vô hạn \(\left( {{u_n}} \right)\) có công bội q thỏa mãn \(\left| q \right| < 1\) được gọi là cấp số nhân lùi vô hạn. Cấp số nhân lùi vô hạn này có tổng là: \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\)
Lời giải chi tiết
Độ dài cạnh của các hình vuông lần lượt là:
\({a_1} = \frac{1}{2},{a_2} = \frac{1}{2}{a_1} = \frac{1}{2}.\frac{1}{2} = {\left( {\frac{1}{2}} \right)^2},{a_3} = \frac{1}{2}{a_2} = \frac{1}{2}{\left( {\frac{1}{2}} \right)^2} = {\left( {\frac{1}{2}} \right)^3},...\)
Diện tích của các hình vuông lần lượt là:
\({S_1} = a_1^2 = {\left( {\frac{1}{2}} \right)^2} = \frac{1}{4},\)
\({S_2} = a_2^2 = {\left( {{{\left( {\frac{1}{2}} \right)}^2}} \right)^2} = {\left( {\frac{1}{4}} \right)^2},\)
\({S_3} = a_3^2 = {\left( {{{\left( {\frac{1}{2}} \right)}^3}} \right)^2} = {\left( {\frac{1}{4}} \right)^3},...\)
Các diện tích \({S_1},{S_2},{S_3},...\) lập thành một cấp số nhân lùi vô hạn với số hạng đầu là \({S_1} = \frac{1}{4}\) và công bội bằng \(\frac{1}{4}\).
Do đó, tổng diện tích các hình vuông là: \(S = \frac{1}{4}.\frac{1}{{1 - \frac{1}{4}}} = \frac{1}{3}\)
Bài 12 trang 77 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về phép biến hình. Bài tập này yêu cầu học sinh vận dụng kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán liên quan đến biến đổi hình học.
Bài 12 bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết cho từng câu hỏi:
Đề bài: Cho điểm A(1; 2). Tìm ảnh A' của điểm A qua phép tịnh tiến theo vectơ v = (3; -1).
Lời giải:
Sử dụng công thức phép tịnh tiến: A'(x' ; y') = A(x; y) + v(a; b) = (x + a; y + b)
Thay các giá trị vào, ta có: A'(1 + 3; 2 - 1) = A'(4; 1)
Vậy, ảnh A' của điểm A qua phép tịnh tiến theo vectơ v = (3; -1) là A'(4; 1).
Đề bài: Cho đường thẳng d: x + y - 2 = 0. Tìm ảnh d' của đường thẳng d qua phép quay tâm O, góc 90°.
Lời giải:
Để tìm ảnh của đường thẳng d qua phép quay tâm O, góc 90°, ta cần tìm hai điểm thuộc d và tìm ảnh của chúng qua phép quay. Sau đó, vẽ đường thẳng đi qua hai điểm ảnh này, đó chính là d'.
Chọn hai điểm A(0; 2) và B(2; 0) thuộc đường thẳng d.
Tìm ảnh A' và B' của A và B qua phép quay tâm O, góc 90°:
A'( -2; 0) và B'(0; 2)
Phương trình đường thẳng d' đi qua A' và B' là: x + y - 2 = 0
Vậy, ảnh d' của đường thẳng d qua phép quay tâm O, góc 90° là x + y - 2 = 0.
Phép biến hình có nhiều ứng dụng trong thực tế, như:
Bài 12 trang 77 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về phép biến hình. Hy vọng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn trong quá trình học tập và giải quyết các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Chúc các em học tập tốt!