Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 11 trang 91 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài giải chi tiết dưới đây!
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{x^2} + {\left( {y - 1} \right)^2} = 1\). Với mỗi số thực m, gọi Q(m) là số giao điểm của đường thẳng \(d:y = m\) với đường tròn (C). Viết công thức xác định hàm số \(y = Q\left( m \right)\). Hàm số này không liên tục tại các điểm nào?
Đề bài
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{x^2} + {\left( {y - 1} \right)^2} = 1\). Với mỗi số thực m, gọi Q(m) là số giao điểm của đường thẳng \(d:y = m\) với đường tròn (C). Viết công thức xác định hàm số \(y = Q\left( m \right)\). Hàm số này không liên tục tại các điểm nào?
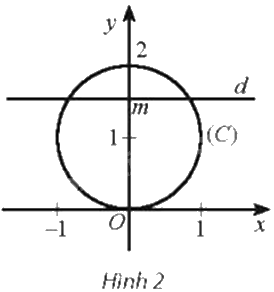
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về định nghĩa hàm số liên tục tại một điểm để xét tính liên tục của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng K và \({x_0} \in K\). Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại điểm \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
Lời giải chi tiết
\(Q\left( m \right) = \left\{ \begin{array}{l}0\;khi\;m < 0\;hay\;m > 2\\1\;khi\;m = 0\;hay\;m = 2\\2\;khi\;0 < m < 2\end{array} \right.\)
Vì \(\mathop {\lim }\limits_{m \to {0^ + }} Q\left( m \right) \ne \mathop {\lim }\limits_{m \to {0^ - }} Q\left( m \right)\) nên hàm số trên không liên tục tại điểm \(m = 0\).
Vì \(\mathop {\lim }\limits_{m \to {2^ + }} Q\left( m \right) \ne \mathop {\lim }\limits_{m \to {2^ - }} Q\left( m \right)\) nên hàm số trên không liên tục tại điểm \(m = 2\).
Vậy hàm số Q(m) không liên tục tại các điểm \(m = 0\), \(m = 2\).
Bài 11 trang 91 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững kiến thức về:
Nội dung bài tập:
Bài 11 yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai, tìm tọa độ đỉnh của parabol, vẽ đồ thị hàm số và khảo sát sự biến thiên của hàm số.
Để giải bài 11 trang 91 sách bài tập Toán 11 Chân trời sáng tạo tập 1, chúng ta sẽ thực hiện các bước sau:
Ví dụ minh họa:
Giả sử hàm số được cho là y = 2x2 - 4x + 1.
Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số và khảo sát sự biến thiên của hàm số.
Kết luận:
Bài 11 trang 91 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Chúc các em học tập tốt!