Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 4 trang 73 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp cho bạn các bước giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và đầy đủ nhất, đồng thời trình bày một cách rõ ràng, logic để bạn có thể dễ dàng theo dõi và áp dụng vào các bài tập tương tự.
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\). Tam giác ABC vuông tại A, \(\widehat {ABC} \) \( = {30^0}\), \(AC \) \( = a,SA \) \( = \frac{{a\sqrt 3 }}{2}\).
Đề bài
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\). Tam giác ABC vuông tại A, \(\widehat {ABC} \) \( = {30^0}\), \(AC \) \( = a,SA \) \( = \frac{{a\sqrt 3 }}{2}\). Tính số đo góc phẳng nhị diện \(\left[ {S,BC,A} \right]\).
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về góc nhị diện: Cho hai nửa mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{Q_1}} \right)\) có chung bờ là đường thẳng d. Hình tạo bởi \(\left( {{P_1}} \right)\), \(\left( {{Q_1}} \right)\) và d được gọi là góc nhị diện tạo bởi \(\left( {{P_1}} \right)\) và \(\left( {{Q_1}} \right)\), kí hiệu \(\left[ {{P_1},d,{Q_1}} \right]\).
+ Sử dụng kiến thức về góc phẳng nhị diện để tính: Góc phẳng nhị diện của góc nhị diện có đỉnh nằm trên cạnh của nhị diện, có hai cạnh lần lượt nằm trên hai mặt của nhị diện và vuông góc với cạnh của nhị diện.
Lời giải chi tiết
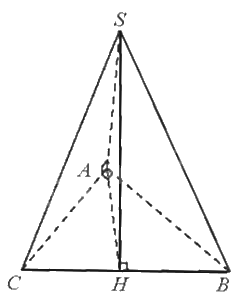
Vẽ \(AH \bot BC\left( {H \in BC} \right)\).
Vì \(SA \bot \left( {ABC} \right) \) \( \Rightarrow SA \bot BC\), mà \(AH \bot BC\) nên \(BC \bot \left( {SHA} \right)\)
Do đó, \(SH \bot BC\) nên góc SHA là góc phẳng nhị diện \(\left[ {S,BC,A} \right]\)
Tam giác AHC vuông tại C nên \(AH \) \( = AC.\sin \widehat {ACB} \) \( = a.\sin {60^0} \) \( = \frac{{a\sqrt 3 }}{2}\)
Vì \(SA \bot \left( {ABC} \right)\) nên \(SA \bot AH \) \( \Rightarrow \widehat {SAH} \) \( = {90^0}\), mà \(AH \) \( = SA\left( { = \frac{{a\sqrt 3 }}{2}} \right)\) nên tam giác SAH vuông cân tại A. Do đó, \(\widehat {SHA} \) \( = {45^0}\)
Bài 4 trang 73 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các công thức đạo hàm cơ bản, quy tắc tính đạo hàm của hàm số hợp, và khả năng áp dụng đạo hàm để tìm cực trị, khoảng đơn điệu của hàm số.
Bài 4 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 4 trang 73, chúng ta sẽ đi vào phân tích từng dạng bài tập cụ thể.
Để tính đạo hàm của hàm số, chúng ta cần áp dụng các công thức đạo hàm cơ bản và quy tắc tính đạo hàm của hàm số hợp. Ví dụ, nếu hàm số có dạng y = f(x), thì đạo hàm của hàm số là y' = f'(x). Nếu hàm số có dạng y = u(v(x)), thì đạo hàm của hàm số là y' = u'(v(x)) * v'(x).
Để tìm cực trị của hàm số, chúng ta cần tìm các điểm mà đạo hàm của hàm số bằng 0 hoặc không tồn tại. Sau đó, chúng ta cần xét dấu của đạo hàm để xác định xem các điểm đó là điểm cực đại hay điểm cực tiểu. Nếu đạo hàm đổi dấu từ dương sang âm tại một điểm, thì điểm đó là điểm cực đại. Nếu đạo hàm đổi dấu từ âm sang dương tại một điểm, thì điểm đó là điểm cực tiểu.
Để xác định khoảng đơn điệu của hàm số, chúng ta cần xét dấu của đạo hàm. Nếu đạo hàm dương trên một khoảng, thì hàm số đồng biến trên khoảng đó. Nếu đạo hàm âm trên một khoảng, thì hàm số nghịch biến trên khoảng đó.
Trong các bài toán thực tế, đạo hàm có thể được sử dụng để giải quyết các vấn đề liên quan đến tối ưu hóa, tốc độ thay đổi, và các bài toán liên quan đến hình học. Ví dụ, chúng ta có thể sử dụng đạo hàm để tìm kích thước của một hình hộp chữ nhật có thể tích lớn nhất với một diện tích bề mặt cho trước.
Khi giải bài 4 trang 73, các em cần lưu ý những điều sau:
Bài 4 trang 73 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải toán. Hy vọng rằng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin hơn trong quá trình học tập và đạt được kết quả tốt nhất.
| Công thức | Mô tả |
|---|---|
| (xn)' = nxn-1 | Đạo hàm của lũy thừa |
| (sin x)' = cos x | Đạo hàm của sin x |
| (cos x)' = -sin x | Đạo hàm của cos x |