Bài 2 trang 117 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về kiến thức đã học. Bài tập này thường yêu cầu vận dụng các công thức, định lý đã được trình bày trong sách giáo khoa.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp các em học sinh có thể tự học và nắm vững kiến thức một cách hiệu quả.
Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\); I, J lần lượt là trung điểm của BD, CD. a) Chứng minh rằng MN//BC. b) Tứ giác MNJI là hình gì. Tìm điều kiện để tứ giác MNJI là hình bình hành.
Đề bài
Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\); I, J lần lượt là trung điểm của BD, CD.
a) Chứng minh rằng MN//BC.
b) Tứ giác MNJI là hình gì. Tìm điều kiện để tứ giác MNJI là hình bình hành.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để chứng minh: Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
Lời giải chi tiết
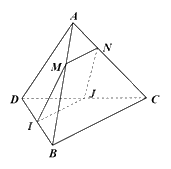
a) Tam giác ABC có: \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) nên MN//BC (định lí Thalès đảo)
b) Vì I, J lần lượt là trung điểm của BD, CD nên IJ là đường trung bình của tam giác BCD. Do đó, IJ//BC
Mà MN//BC nên IJ//MN, do đó, MNJI là hình thang.
Hình thang MNJI là hình bình hành khi và chỉ khi MI//NJ//AD.
Mà I là trung điểm của BD. Do đó, MI là đường trung bình của tam giác ADB.
Suy ra M là trung điểm của AB.
Bài 2 trang 117 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc tính đạo hàm của hàm số, tìm điểm cực trị, và khảo sát hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Trước khi bắt tay vào giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Sau đó, cần phân tích bài toán để tìm ra phương pháp giải phù hợp. Đối với bài 2 trang 117, phương pháp giải thường bao gồm:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:
Bài 2: (Giả sử đề bài là: Tìm đạo hàm của hàm số f(x) = x^3 - 2x^2 + 5x - 1)
Lời giải:
Áp dụng các quy tắc tính đạo hàm, ta có:
f'(x) = 3x^2 - 4x + 5
Vậy, đạo hàm của hàm số f(x) = x^3 - 2x^2 + 5x - 1 là f'(x) = 3x^2 - 4x + 5.
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, học sinh có thể luyện tập thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Dưới đây là một số bài tập gợi ý:
Để học toán hiệu quả, học sinh cần:
Bài 2 trang 117 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm. Hy vọng với lời giải chi tiết và các lời khuyên trên, các em học sinh có thể tự học và nắm vững kiến thức một cách hiệu quả. Chúc các em học tốt!