Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 158 sách bài tập Toán 11 - Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Thâm niên công tác của các công nhân hai nhà máy A và B. a) Hãy so sánh thâm niên công tác của nhân viên hai nhà máy theo số trung bình và trung vị. b) Hãy ước lượng tứ phân vị thứ nhất và thứ ba của hai mẫu số liệu ghép nhóm trên.
Đề bài
Thâm niên công tác của các công nhân hai nhà máy A và B.

a) Hãy so sánh thâm niên công tác của nhân viên hai nhà máy theo số trung bình và trung vị.
b) Hãy ước lượng tứ phân vị thứ nhất và thứ ba của hai mẫu số liệu ghép nhóm trên.
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về số trung bình của mẫu số liệu để tính:
Giả sử mẫu số được cho dưới dạng bảng tần số ghép nhóm:
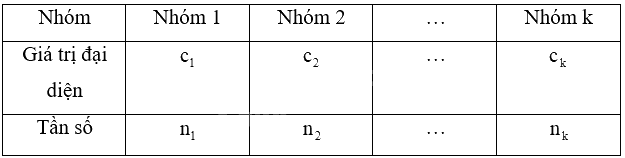
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).
b) + Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính:
Gọi n là cỡ mẫu.
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị, \({n_m}\) là tần số của nhóm chứa trung vị,
\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, trung vị của mẫu số liệu là: \({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
+ Sử dụng kiến thức về xác định tứ phân vị của mẫu số liệu ghép nhóm để tính:
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm, kí hiệu \({Q_2}\), cũng chính là trung vị của mẫu số liệu ghép nhóm.
Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất, \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất, \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\)
Khi đó, tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
Để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu \({Q_3}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_j};{u_{j + 1}}} \right)\) chứa tứ phân vị thứ ba, \({n_j}\) là tần số của nhóm chứa tứ phân vị thứ ba, \(C = {n_1} + {n_2} + ... + {n_{j - 1}}\)
Khi đó, tứ phân vị thứ ba của mẫu số liệu là: \({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right)\)
Lời giải chi tiết
a) Bảng tần số ghép nhóm bao gồm giá trị đại diện là:
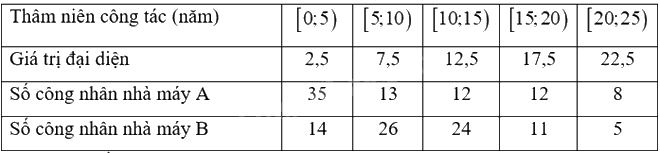
Trung bình số năm thâm niên của công nhân nhà máy A là:
\(\overline {{x_A}} = \frac{{2,5.35 + 7,5.13 + 12,5.12 + 17,5.12 + 22,5.8}}{{35 + 13 + 12 + 12 + 8}} = 9,0625\) (năm)
Trung bình số năm thâm niên của công nhân nhà máy B là:
\(\overline {{x_B}} = \frac{{2,5.14 + 7,5.26 + 12,5.24 + 17,5.11 + 22,5.5}}{{14 + 26 + 24 + 11 + 5}} = 10,4375\) (năm)
Vậy nếu so sánh theo số trung bình (năm) thì thâm niên công tác của nhân viên công ty A ngắn hơn thâm niên công tác của nhân viên công ty B.
Nhà máy A:
Cỡ mẫu \(n = 80\)
Gọi \({x_1},{x_2},...,{x_{80}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_{35}} \in \left[ {0;5} \right),{x_{36}},...,{x_{48}} \in \left[ {5;10} \right),{x_{49}},...,{x_{60}} \in \left[ {10;15} \right),\)
\({x_{61}},...,{x_{72}} \in \left[ {15;20} \right),{x_{73}},...,{x_{80}} \in \left[ {20;25} \right)\).
Do cỡ mẫu \(n = 80\) nên trung vị của mẫu số liệu là \(\frac{1}{2}\left( {{x_{40}} + {x_{41}}} \right)\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {5;10} \right)\).
Trung vị của mẫu số liệu ghép nhóm là: \({M_e}\left( A \right) = 5 + \frac{{\frac{{80}}{2} - 35}}{{13}}.\left( {10 - 5} \right) = \frac{{90}}{{13}}\)
Nhà máy B:
Cỡ mẫu \(n = 80\)
Gọi \({x_1},{x_2},...,{x_{80}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_{14}} \in \left[ {0;5} \right),{x_{15}},...,{x_{40}} \in \left[ {5;10} \right),{x_{41}},...,{x_{64}} \in \left[ {10;15} \right),\)
\({x_{65}},...,{x_{75}} \in \left[ {15;20} \right),{x_{76}},...,{x_{80}} \in \left[ {20;25} \right)\)
Do cỡ mẫu \(n = 80\) nên trung vị của mẫu số liệu là \(\frac{1}{2}\left( {{x_{40}} + {x_{41}}} \right)\). Do \({x_{40}} \in \left[ {5;10} \right),{x_{41}} \in \left[ {10;15} \right)\) nên ta có trung vị là \({M_e}\left( B \right) = 10\)
Vì \(\frac{{90}}{{13}} < 10\) nên nếu so sánh theo trung vị thì thâm niên công tác của nhân viên công ty A ngắn hơn thâm niên công tác của nhân viên công ty B.
b) Nhà máy A:
Do cỡ mẫu \(n = 80\) nên tứ phân vị thứ nhất của mẫu số liệu là \(\frac{1}{2}\left( {{x_{20}} + {x_{21}}} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {0;5} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1}\left( A \right) = 0 + \frac{{\frac{{80}}{4} - 0}}{{35}}.\left( {5 - 0} \right) = \frac{{20}}{7}\)
Do cỡ mẫu \(n = 80\) nên tứ phân vị thứ ba của mẫu số liệu là \(\frac{1}{2}\left( {{x_{60}} + {x_{61}}} \right)\). Do \({x_{60}} \in \left[ {10;15} \right),{x_{61}} \in \left[ {15;20} \right)\) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là \({Q_3}\left( A \right) = 15\).
Nhà máy B:
Do cỡ mẫu \(n = 80\) nên tứ phân vị thứ nhất của mẫu số liệu là \(\frac{1}{2}\left( {{x_{20}} + {x_{21}}} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {5;10} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}\left( B \right) = 5 + \frac{{\frac{{80}}{4} - 14}}{{26}}.\left( {10 - 5} \right) = \frac{{80}}{{13}}\)
Do cỡ mẫu \(n = 80\) nên tứ phân vị thứ ba của mẫu số liệu là \(\frac{1}{2}\left( {{x_{60}} + {x_{61}}} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu thuộc nhóm \(\left[ {10;15} \right)\) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}\left( B \right) = 10 + \frac{{\frac{{3.80}}{4} - \left( {14 + 26} \right)}}{{24}}.\left( {15 - 10} \right) = \frac{{85}}{6}\)
Bài 3 trang 158 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 thuộc chương trình học về phép biến hình. Bài tập này tập trung vào việc vận dụng các kiến thức đã học về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán thực tế.
Bài 3 bao gồm các dạng bài tập sau:
Để giải phần a, ta cần xác định ảnh của điểm M qua phép tịnh tiến theo vectơ v. Sử dụng công thức: M' = M + v, ta sẽ tìm được tọa độ của điểm M'.
Phần b yêu cầu tìm tâm của phép quay biến điểm A thành điểm B. Ta sử dụng công thức tìm tâm quay O: OA = OB và góc AOB bằng góc tạo bởi hai vectơ OA và OB.
Để chứng minh tam giác ABC là ảnh của tam giác A'B'C' qua phép đối xứng trục Oy, ta cần chứng minh rằng mỗi đỉnh của tam giác ABC là ảnh của một đỉnh tương ứng của tam giác A'B'C' qua phép đối xứng trục Oy.
Để giải tốt các bài tập về phép biến hình, các em cần nắm vững các kiến thức sau:
Ví dụ 1: Cho điểm A(1; 2) và vectơ v = (3; -1). Tìm tọa độ của điểm A' là ảnh của A qua phép tịnh tiến theo vectơ v.
Lời giải: A' = A + v = (1 + 3; 2 - 1) = (4; 1).
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ hiểu rõ hơn về bài 3 trang 158 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 và có thể tự tin giải quyết các bài tập tương tự. Chúc các em học tập tốt!