Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 5 trang 159 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
Kết quả kiểm tra cân nặng của một số quả trứng chim cút được lựa chọn ngẫu nhiên ở hai trang trại chăn nuôi A và B được biểu diễn ở biểu đồ sau (đơn vị: g). a) Hãy so sánh cân nặng của trứng chim cút của hai trang trại A và B theo số trung bình và trung vị. b) Hãy ước lượng tứ phân vị thứ nhất và tứ phân vị thứ ba của cân nặng trứng chim cút của trang trại A.
Đề bài
Kết quả kiểm tra cân nặng của một số quả trứng chim cút được lựa chọn ngẫu nhiên ở hai trang trại chăn nuôi A và B được biểu diễn ở biểu đồ sau (đơn vị: g).
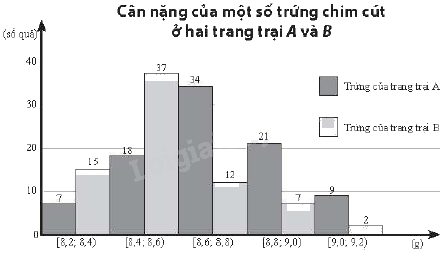
a) Hãy so sánh cân nặng của trứng chim cút của hai trang trại A và B theo số trung bình và trung vị.
b) Hãy ước lượng tứ phân vị thứ nhất và tứ phân vị thứ ba của cân nặng trứng chim cút của trang trại A.
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về số trung bình của mẫu số liệu để so sánh:
Giả sử mẫu số được cho dưới dạng bảng tần số ghép nhóm:
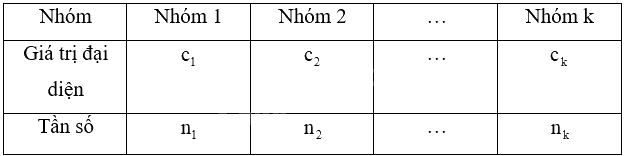
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).
+ Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính:
Gọi n là cỡ mẫu.
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị, \({n_m}\) là tần số của nhóm chứa trung vị,
\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, trung vị của mẫu số liệu là: \({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
b) Sử dụng kiến thức về xác định tứ phân vị của mẫu số liệu ghép nhóm để tính:
Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất, \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất, \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\)
Khi đó, tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
Để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu \({Q_3}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_j};{u_{j + 1}}} \right)\) chứa tứ phân vị thứ ba, \({n_j}\) là tần số của nhóm chứa tứ phân vị thứ ba, \(C = {n_1} + {n_2} + ... + {n_{j - 1}}\)
Khi đó, tứ phân vị thứ ba của mẫu số liệu là: \({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right)\)
Lời giải chi tiết
a) Từ biểu đồ đã cho, ta có bảng số liệu ghép nhóm (bao gồm cả giá trị đại diện):
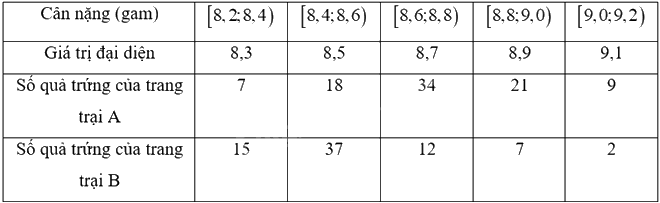
Đối với trang trại A: Cỡ mẫu: \({n_A} = 89\)
Cân nặng trung bình của mỗi quả trứng là: \(\overline {{x_A}} = \frac{{8,3.7 + 8,5.18 + 8,7.34 + 8,9.21 + 9,1.9}}{{89}} = \frac{{7\;757}}{{890}}\)
Gọi \({x_1},{x_2},...,{x_{89}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_7} \in \left[ {8,2;8,4} \right),{x_8},...,{x_{25}} \in \left[ {8,4;8,6} \right),{x_{26}},...,{x_{59}} \in \left[ {8,6;8,8} \right),\)\({x_{60}},...,{x_{80}} \in \left[ {8,8;9,0} \right),{x_{81}},...,{x_{89}} \in \left[ {9,0;9,2} \right)\)
Do cỡ mẫu \({n_A} = 89\) nên trung vị \({M_e}\left( A \right) = {x_{45}} \in \left[ {8,6;8,8} \right)\) nên trung vị của mẫu số liệu là: \({M_e}\left( A \right) = 8,6 + \frac{{\frac{{89}}{2} - \left( {7 + 18} \right)}}{{34}}.\left( {8,8 - 8,6} \right) = \frac{{2\;963}}{{340}}\) (g)
Đối với trang trại B: Cỡ mẫu: \({n_B} = 73\)
Cân nặng trung bình của mỗi quả trứng là:
\(\overline {{x_B}} = \frac{{8,3.15 + 8,5.37 + 8,7.12 + 8,9.7 + 9,1.2}}{{73}} = \frac{{6\;239}}{{730}}\) (g)
Gọi \({x_1},{x_2},...,{x_{73}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_{15}} \in \left[ {8,2;8,4} \right),{x_{16}},...,{x_{52}} \in \left[ {8,4;8,6} \right),{x_{53}},...,{x_{64}} \in \left[ {8,6;8,8} \right),\) \({x_{65}},...,{x_{71}} \in \left[ {8,8;9,0} \right),{x_{72}},{x_{73}} \in \left[ {9,0;9,2} \right)\)
Do cỡ mẫu \({n_B} = 73\) nên trung vị \({M_e}\left( B \right) = {x_{37}} \in \left[ {8,4;8,6} \right)\) nên trung vị của mẫu số liệu là: \({M_e}\left( B \right) = 8,4 + \frac{{\frac{{73}}{2} - 15}}{{37}}.\left( {8,6 - 8,4} \right) = \frac{{3\;151}}{{370}}\) (g)
Vì \(\overline {{x_A}} > \overline {{x_B}} ,{M_e}\left( A \right) > {M_e}\left( B \right)\) nên so sánh theo số trung bình hay trung vị thì cân nặng của trứng chim cút của trang trại A đều hơn cân nặng của trứng chim cút của trang trại B
b) Đối với trang trại A:
Do cỡ mẫu \({n_A} = 89\) nên tứ phân vị thứ nhất của mẫu số liệu là \(\frac{1}{2}\left( {{x_{22}} + {x_{23}}} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {8,4;8,6} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1}\left( A \right) = 8,4 + \frac{{\frac{{89}}{4} - 7}}{{18}}.\left( {8,6 - 8,4} \right) = \frac{{617}}{{72}}\)
Do cỡ mẫu \({n_A} = 89\) nên tứ phân vị thứ ba của mẫu số liệu là \(\frac{1}{2}\left( {{x_{67}} + {x_{68}}} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu thuộc nhóm \(\left[ {8,8;9,0} \right)\).
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3}\left( A \right) = 8,8 + \frac{{\frac{{3.89}}{4} - \left( {7 + 18 + 34} \right)}}{{21}}.\left( {9,0 - 8,8} \right) = \frac{{3\;727}}{{420}}\)
Bài 5 trang 159 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, các quy tắc tính đạo hàm và các ứng dụng của đạo hàm.
Bài 5 trang 159 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. Lưu ý rằng, đây chỉ là một trong nhiều cách giải bài tập. Bạn có thể tìm hiểu thêm các cách giải khác để mở rộng kiến thức của mình.
Để tính đạo hàm của hàm số tại một điểm, ta sử dụng công thức:
f'(x0) = limh→0 (f(x0 + h) - f(x0)) / h
Trong đó:
Ví dụ, để tính đạo hàm của hàm số f(x) = x2 tại điểm x = 2, ta thực hiện như sau:
f'(2) = limh→0 ((2 + h)2 - 22) / h = limh→0 (4 + 4h + h2 - 4) / h = limh→0 (4h + h2) / h = limh→0 (4 + h) = 4
Vậy, đạo hàm của hàm số f(x) = x2 tại điểm x = 2 là 4.
Để tìm đạo hàm của hàm số, ta sử dụng các quy tắc tính đạo hàm. Một số quy tắc tính đạo hàm cơ bản bao gồm:
Ví dụ, để tìm đạo hàm của hàm số f(x) = 3x2 + 2x - 1, ta thực hiện như sau:
f'(x) = 3 * 2x1 + 2 * 1 - 0 = 6x + 2
Vậy, đạo hàm của hàm số f(x) = 3x2 + 2x - 1 là 6x + 2.
Đạo hàm có nhiều ứng dụng trong thực tế, chẳng hạn như:
Ví dụ, để tìm vận tốc của một vật chuyển động theo hàm số s(t) = t2 + 2t, ta tính đạo hàm của hàm số s(t) theo thời gian t:
v(t) = s'(t) = 2t + 2
Vậy, vận tốc của vật tại thời điểm t là 2t + 2.
Khi giải bài tập về đạo hàm, bạn cần lưu ý những điều sau:
Hy vọng rằng, với lời giải chi tiết và những lưu ý trên, bạn đã có thể giải bài 5 trang 159 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!