Bài 4 trang 161 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh tính đạo hàm, tìm cực trị, và vẽ đồ thị hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 161, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một cửa hàng sách thống kê số truyện thiếu nhi bán được trong hai tháng ở bảng sau: Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên.
Đề bài
Một cửa hàng sách thống kê số truyện thiếu nhi bán được trong hai tháng ở bảng sau:

Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về số trung bình của mẫu số liệu để tính:
Giả sử mẫu số được cho dưới dạng bảng tần số ghép nhóm:
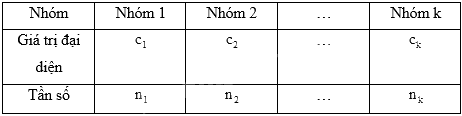
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).
+ Sử dụng kiến thức về mốt của mẫu số liệu để tính: Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_O}\) được xác định bởi công thức: \({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
+ Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính:
Gọi n là cỡ mẫu.
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị, \({n_m}\) là tần số của nhóm chứa trung vị,
\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, trung vị của mẫu số liệu là: \({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
+ Sử dụng kiến thức về xác định tứ phân vị của mẫu số liệu ghép nhóm để tính:
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm, kí hiệu \({Q_2}\), cũng chính là trung vị của mẫu số liệu ghép nhóm.
Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất, \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất, \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\)
Khi đó, tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
Để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu \({Q_3}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_j};{u_{j + 1}}} \right)\) chứa tứ phân vị thứ ba, \({n_j}\) là tần số của nhóm chứa tứ phân vị thứ ba, \(C = {n_1} + {n_2} + ... + {n_{j - 1}}\)
Khi đó, tứ phân vị thứ ba của mẫu số liệu là: \({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right)\)
Lời giải chi tiết
Ta hiệu chỉnh được bảng tần số ghép nhóm gồm các giá trị đại diện của nhóm là:

Cỡ mẫu \(n = 61\)
Số trung bình của mẫu số liệu là: \(\overline x = \frac{{17.5 + 24.7 + 31.25 + 38.15 + 45.9}}{{61}} = \frac{{2\;003}}{{61}}\)
Nhóm chứa mốt của mẫu số liệu là \(\left[ {27,5;34,5} \right)\).
Do đó, \({u_m} = 27,5,{u_{m + 1}} = 34,5,{n_m} = 25,{n_{m + 1}} = 15,{u_{m + 1}} - {u_m} = 34,5 - 27,5 = 7\)
Mốt của mẫu số liệu là: \({M_O} = 27,5 + \frac{{25 - 7}}{{\left( {25 - 7} \right) + \left( {25 - 15} \right)}}.7 = 32\)
Gọi \({x_1},{x_2},...,{x_{61}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_5} \in \left[ {13,5;20,5} \right),{x_6},...,{x_{12}} \in \left[ {20,5;27,5} \right),{x_{13}},...,{x_{37}} \in \left[ {27,5;34,5} \right),\) \({x_{38}},...,{x_{52}} \in \left[ {34,5;41,5} \right),{x_{53}},...,{x_{61}} \in \left[ {41,5;48,5} \right)\).
Do cỡ mẫu \(n = 61\) nên tứ phân vị thứ hai của mẫu số liệu là \({x_{31}}\). Do đó tứ phân vị thứ hai của mẫu số liệu thuộc nhóm \(\left[ {27,5;34,5} \right)\).
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm là:
\({Q_2} = 27,5 + \frac{{\frac{{61}}{2} - \left( {5 + 7} \right)}}{{25}}.\left( {34,5 - 27,5} \right) = \frac{{817}}{{25}}\)
Do cỡ mẫu \(n = 61\) nên tứ phân vị thứ nhất của mẫu số liệu là \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {27,5;34,5} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 27,5 + \frac{{\frac{{61}}{4} - \left( {5 + 7} \right)}}{{25}}.\left( {34,5 - 27,5} \right) = 28,41\)
Do cỡ mẫu \(n = 61\) nên tứ phân vị thứ ba của mẫu số liệu là \(\frac{1}{2}\left( {{x_{46}} + {x_{47}}} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu thuộc nhóm \(\left[ {34,5;41,5} \right)\).
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 34,5 + \frac{{\frac{{3.61}}{4} - \left( {5 + 7 + 25} \right)}}{{15}}.\left( {41,5 - 34,5} \right) = \frac{{463}}{{12}}\)
Bài 4 trang 161 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
Trước khi đi vào lời giải cụ thể, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Thông thường, bài 4 trang 161 sẽ yêu cầu học sinh thực hiện các bước sau:
Ví dụ minh họa (Giả sử bài toán cụ thể là hàm số f(x) = x3 - 3x2 + 2):
Ngoài bài 4 trang 161, học sinh có thể gặp các dạng bài tập tương tự như:
Để giải nhanh các bài tập này, học sinh nên:
Để hiểu sâu hơn về đạo hàm và ứng dụng của đạo hàm, học sinh có thể tham khảo các tài liệu sau:
Bài 4 trang 161 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Bằng cách nắm vững các kiến thức cơ bản, phân tích kỹ đề bài, và luyện tập thường xuyên, học sinh có thể tự tin giải quyết bài toán này và các bài toán tương tự.