Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh 2a. Mặt phẳng (B’AC) tạo với đáy một góc \({30^0}\), khoảng cách từ B đến mặt phẳng (D’AC) bằng \(\frac{a}{2}\). Tính thể tích khối tứ diện ACB’D’.
Đề bài
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh 2a. Mặt phẳng (B’AC) tạo với đáy một góc \({30^0}\), khoảng cách từ B đến mặt phẳng (D’AC) bằng \(\frac{a}{2}\). Tính thể tích khối tứ diện ACB’D’.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng.
+ Sử dụng kiến thức về thể tích khối tứ diện.
Lời giải chi tiết
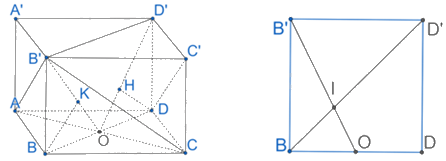
Gọi O là giao điểm của AC và BD.
Ta có: \(AC \bot BD,AC \bot BB' \) \( \Rightarrow AC \bot \left( {BB'D} \right) \) \( \Rightarrow AC \bot B'O\)
Khi đó, \(BO \bot AC,B'O \bot AC,BO \subset \left( {ABCD} \right),B'O \subset \left( {B'AC} \right)\), AC là giao tuyến của (B’AC) và (ABCD). Do đó, \(\left( {\left( {B'AC} \right),\left( {ABCD} \right)} \right) = \left( {BO,B'O} \right) = \widehat {B'OB} = {30^0}\)
Ta có: \(d\left( {B,\left( {D'AC} \right)} \right) = d\left( {D,\left( {D'AC} \right)} \right) = \frac{a}{2}\)
Chứng minh được: \(AC \bot \left( {BB'D'D} \right) \) \( \Rightarrow \left( {D'AC} \right) \bot \left( {BB'D'D} \right)\) và D’O là giao tuyến của (D’AC) và (BB’D’D).
Từ D kẻ \(DH \bot D'O\left( {H \in D'O} \right)\). Do đó, \(d\left( {D,\left( {D'AC} \right)} \right) = DH = \frac{a}{2}\)
Xét tam giác B’OB vuông tại B có: \(\frac{{BB'}}{{BO}} = \tan {30^0} \) \( \Rightarrow OD = BO = \sqrt 3 BB'\)
Xét tam giác D’DO vuông tại D, đường cao DH có:
\(\frac{1}{{D{H^2}}} = \frac{1}{{O{D^2}}} + \frac{1}{{D'{D^2}}} \) \( \Rightarrow \frac{4}{{{a^2}}} = \frac{1}{{3BB{'^2}}} + \frac{1}{{D'{D^2}}} \) \( \Rightarrow D'D = \frac{{a\sqrt 3 }}{3} \) \( \Rightarrow OB = a\)
Gọi I là giao điểm của BD’ và B’O, suy ra: \(\frac{{BI}}{{D'I}} = \frac{1}{2} \) \( \Rightarrow d\left( {D',\left( {B'AC} \right)} \right) = 2d\left( {B,\left( {B'AC} \right)} \right) \) \( \Rightarrow {V_{ACB'D'}} = 2{V_{B'ABC}}\)
Tam giác AOB vuông tại O có: \(OA = \sqrt {A{B^2} - O{B^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \)
Diện tích tam giác ABC là: \({S_{ABC}} = 2{S_{ABO}} = 2.\frac{1}{2}.OB.OA = {a^2}\sqrt 3 \)
Suy ra: \({V_{B'ABC}} = \frac{1}{3}BB'.{S_{ABC}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{3}.{a^2}\sqrt 3 = \frac{{{a^3}}}{3}\). Vậy \({V_{ACB'D'}} = \frac{{2{a^3}}}{3}\)
Bài 7 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của tổng, hiệu, tích, thương của các hàm số. Việc nắm vững các quy tắc này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài 7 bao gồm các bài tập yêu cầu học sinh:
Cho hàm số f(x) = x^3 + 2x^2 - 5x + 1. Tính f'(x).
Lời giải:
Áp dụng quy tắc đạo hàm của tổng, hiệu, lũy thừa, ta có:
f'(x) = 3x^2 + 4x - 5
Cho hàm số g(x) = (x^2 + 1)(x - 2). Tính g'(x).
Lời giải:
Áp dụng quy tắc đạo hàm của tích, ta có:
g'(x) = (2x)(x - 2) + (x^2 + 1)(1) = 2x^2 - 4x + x^2 + 1 = 3x^2 - 4x + 1
Cho hàm số h(x) = (x + 1) / (x - 1). Tính h'(x).
Lời giải:
Áp dụng quy tắc đạo hàm của thương, ta có:
h'(x) = [(1)(x - 1) - (x + 1)(1)] / (x - 1)^2 = (x - 1 - x - 1) / (x - 1)^2 = -2 / (x - 1)^2
Ngoài việc giải bài tập trong sách bài tập, các em có thể tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế, như:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán online.
Bài 7 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp các em hiểu rõ hơn về quy tắc tính đạo hàm. Hy vọng với lời giải chi tiết và các lưu ý trên, các em sẽ tự tin hơn trong quá trình học tập và giải bài tập.