Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 3 trang 73 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài giải dưới đây để nắm vững kiến thức Toán 11 nhé!
Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng \(\frac{{a\sqrt {15} }}{6}\). Tính số đo góc phẳng nhị diện \(\left[ {S,BC,A} \right]\).
Đề bài
Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng \(\frac{{a\sqrt {15} }}{6}\). Tính số đo góc phẳng nhị diện \(\left[ {S,BC,A} \right]\).
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về góc nhị diện: Cho hai nửa mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{Q_1}} \right)\) có chung bờ là đường thẳng d. Hình tạo bởi \(\left( {{P_1}} \right)\), \(\left( {{Q_1}} \right)\) và d được gọi là góc nhị diện tạo bởi \(\left( {{P_1}} \right)\) và \(\left( {{Q_1}} \right)\), kí hiệu \(\left[ {{P_1},d,{Q_1}} \right]\).
+ Sử dụng kiến thức về góc phẳng nhị diện để tính: Góc phẳng nhị diện của góc nhị diện có đỉnh nằm trên cạnh của nhị diện, có hai cạnh lần lượt nằm trên hai mặt của nhị diện và vuông góc với cạnh của nhị diện.
Lời giải chi tiết
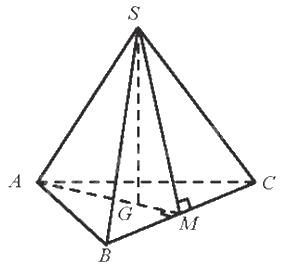
Gọi M là trung điểm của BC, G là trọng tâm của tam giác ABC.
Suy ra, \(SG \bot \left( {ABC} \right),SM \bot BC,AM \bot BC\)
Do đó, góc SMG là góc phẳng nhị diện \(\left[ {S,BC,A} \right]\)
Vì tam giác ABC đều cạnh a nên \(\widehat {ABC} \) \( = {60^0},AB \) \( = a\), AM là đường trung tuyến đồng thời là đường cao. Do đó, tam giác ABM vuông tại M. Suy ra: \(AM \) \( = AB.\sin {60^0} \) \( = \frac{{a\sqrt 3 }}{2}\)
Vì G là trọng tâm tam giác ABC nên \(GM \) \( = \frac{1}{3}AM \) \( = \frac{{a\sqrt 3 }}{6}\)
Vì tam giác SBC đều nên SM là đường trung tuyến đồng thời là đường cao.
Áp dụng định lí Pythagore vào tam giác SBM vuông tại G ta có:
\(SM \) \( = \sqrt {S{B^2} - B{M^2}} \) \( = \frac{{a\sqrt 6 }}{6}\)
Vì \(SG \bot \left( {ABC} \right) \) \( \Rightarrow SG \bot GM\). Áp dụng định lí Pythagore vào tam giác SGM vuông tại G ta có: \(SG \) \( = \sqrt {S{M^2} - G{M^2}} \) \( = \frac{{a\sqrt 3 }}{6}\)
Vì \(GM \) \( = SG\left( { = \frac{{a\sqrt 3 }}{6}} \right),\widehat {SGM} \) \( = {90^0}\) nên tam giác SMG vuông cân tại G.
Do đó, \(\widehat {SMG} \) \( = {45^0}\)
Bài 3 trang 73 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đường thẳng và mặt phẳng trong không gian. Bài tập này yêu cầu học sinh phải nắm vững các định lý, tính chất liên quan đến quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng, cũng như các phương pháp chứng minh trong hình học không gian.
Bài 3 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để giải câu a, ta cần sử dụng định lý về đường thẳng song song với mặt phẳng. Theo định lý này, một đường thẳng song song với một mặt phẳng khi và chỉ khi đường thẳng đó không có điểm chung với mặt phẳng. Để chứng minh đường thẳng song song với mặt phẳng, ta cần chỉ ra rằng đường thẳng đó không nằm trong mặt phẳng và không có điểm chung với mặt phẳng.
(Giải thích chi tiết các bước giải, sử dụng hình vẽ minh họa nếu cần thiết)
Để giải câu b, ta cần sử dụng định lý về đường thẳng vuông góc với mặt phẳng. Theo định lý này, một đường thẳng vuông góc với một mặt phẳng khi và chỉ khi đường thẳng đó vuông góc với mọi đường thẳng nằm trong mặt phẳng. Để chứng minh đường thẳng vuông góc với mặt phẳng, ta cần chỉ ra rằng đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
(Giải thích chi tiết các bước giải, sử dụng hình vẽ minh họa nếu cần thiết)
Câu c yêu cầu tính góc giữa đường thẳng và mặt phẳng. Để tính góc này, ta cần sử dụng công thức tính góc giữa đường thẳng và mặt phẳng. Công thức này liên quan đến hình chiếu của đường thẳng lên mặt phẳng và góc giữa đường thẳng và hình chiếu của nó.
(Giải thích chi tiết các bước giải, sử dụng hình vẽ minh họa nếu cần thiết)
Khi giải các bài tập về đường thẳng và mặt phẳng trong không gian, các em cần lưu ý những điều sau:
Kiến thức về đường thẳng và mặt phẳng trong không gian có ứng dụng rộng rãi trong thực tế, ví dụ như trong kiến trúc, xây dựng, hàng không, vũ trụ. Việc nắm vững kiến thức này sẽ giúp các em hiểu sâu hơn về thế giới xung quanh và có thể giải quyết các vấn đề thực tế một cách hiệu quả.
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự trong sách bài tập Toán 11 - Chân trời sáng tạo tập 2 hoặc trên các trang web học toán online khác.
Hy vọng bài giải chi tiết bài 3 trang 73 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2 này sẽ giúp các em học sinh hiểu rõ hơn về kiến thức và kỹ năng giải bài tập về đường thẳng và mặt phẳng trong không gian. Chúc các em học tập tốt!