Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 11. Bài viết này sẽ hướng dẫn bạn cách giải bài 2 trang 127 sách bài tập toán 11 - Chân trời sáng tạo tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp S. ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của các SA và CD. a) Chứng minh (OMN)//(SBC). b) Giả sử hai tam giác SAD và SAB là các tam giác cân tại A. Gọi AE và AF lần lượt là đường phân giác trong của hai tam giác SAD và SAB. Chứng minh EF//(SBD).
Đề bài
Cho hình chóp S. ABCD có đáy là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm của các SA và CD.
a) Chứng minh (OMN)//(SBC).
b) Giả sử hai tam giác SAD và SAB là các tam giác cân tại A. Gọi AE và AF lần lượt là đường phân giác trong của hai tam giác SAD và SAB. Chứng minh EF//(SBD).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về điều kiện để hai mặt phẳng song song để chứng minh: Nếu mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng (Q) thì (P) song song với (Q).
Lời giải chi tiết
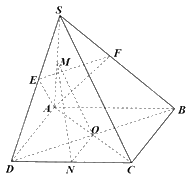
a) Vì ABCD là hình bình hành tâm O nên O là trung điểm của AC, BD.
Vì M, O lần lượt là trung điểm của SA và AC nên MO là đường trung bình của tam giác SAC, suy ra MO//SC. Mà \(SC \subset \left( {SBC} \right)\), MO không nằm trong mặt phẳng (SBC) nên MO//(SBC)
Vì N, O lần lượt là trung điểm của CD và BD nên NO là đường trung bình của tam giác BCD, suy ra NO//BC. Mà \(BC \subset \left( {SBC} \right)\), NO không nằm trong mặt phẳng (SBC) nên NO//(SBC).
Vì MO//(SBC), NO//(SBC), NO và MO cắt nhau tại O và nằm trong mặt phẳng (MNO) nên (OMN)//(SBC).
b) Đề sai vì EF nằm trong mặt phẳng (SBD) rồi nên EF không song song với mặt phẳng (SBD).
Bài 2 trang 127 sách bài tập toán 11 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số lượng giác và đồ thị. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về định nghĩa, tính chất của hàm số lượng giác, cách vẽ đồ thị hàm số và giải các bài toán liên quan đến ứng dụng của hàm số lượng giác.
Bài 2 thường bao gồm các dạng bài tập sau:
Để giải bài 2 trang 127 sách bài tập toán 11 - Chân trời sáng tạo tập 1, chúng ta cần thực hiện các bước sau:
Ví dụ minh họa:
Giả sử bài 2 yêu cầu tìm tập xác định của hàm số y = tan(2x). Để giải bài này, chúng ta cần nhớ rằng hàm số tan(x) xác định khi cos(x) ≠ 0. Do đó, hàm số y = tan(2x) xác định khi cos(2x) ≠ 0. Điều này tương đương với 2x ≠ π/2 + kπ, với k là số nguyên. Suy ra, x ≠ π/4 + kπ/2, với k là số nguyên. Vậy tập xác định của hàm số y = tan(2x) là D = R \ {π/4 + kπ/2, k ∈ Z}.
Khi giải bài tập toán 11 - Chân trời sáng tạo tập 1, bạn cần lưu ý những điều sau:
Kiến thức về hàm số lượng giác và đồ thị có ứng dụng rộng rãi trong nhiều lĩnh vực của khoa học và kỹ thuật, như:
Bài 2 trang 127 sách bài tập toán 11 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số lượng giác và đồ thị. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, bạn sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn toán.
| Hàm số | Tập xác định | Tập giá trị |
|---|---|---|
| y = sin(x) | R | [-1, 1] |
| y = cos(x) | R | [-1, 1] |
| y = tan(x) | R \ {π/2 + kπ, k ∈ Z} | R |