Giải bài 4 trang 112 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1

Giải bài 4 trang 112 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Giải bài 4 trang 112 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1

Bài 4 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Bài tập này thường yêu cầu học sinh phải nắm vững các kiến thức về quy tắc tính đạo hàm, điều kiện cực trị và cách xác định điểm cực trị.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 112, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy các điểm E, F, G sao cho \(EB > AE,AF > FC,BG > GD\). Tìm giao tuyến của các cặp mặt phẳng (EFG) và (ACD), (EFG) và (BCD), (EFG) và (ABD).

Đề bài

Phương pháp giải - Xem chi tiết Giải bài 4 trang 112 sách bài tập toán 11 - Chân trời sáng tạo tập 1 1

Sử dụng kiến thức về giao tuyến giữa hai mặt phẳng để tìm giao tuyến: Đường thẳng d chung giữa hai mặt phẳng (P) và (Q) được gọi là giao tuyến của (P) và (Q), kí hiệu \(d = \left( P \right) \cap \left( Q \right)\).

Lời giải chi tiết

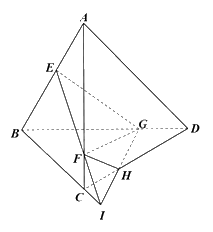
Giải bài 4 trang 112 sách bài tập toán 11 - Chân trời sáng tạo tập 1 2

Ta có, EF là giao tuyến của hai mặt phẳng (EFG) và (ABC).

Trong mặt phẳng (ABC), gọi I là giao điểm của EF và BC.

Trong mặt phẳng (BCD), gọi H là giao điểm của IG và CD.

Vì \(\left\{ \begin{array}{l}H \in CD \subset \left( {ACD} \right),H \in IG \subset \left( {EFG} \right)\\F \in AC \subset \left( {ACD} \right),F \in FE \subset \left( {EFG} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (EFG) và (ACD) là FH.

Vì \(\left\{ \begin{array}{l}H \in CD \subset \left( {BCD} \right),H \in IG \subset \left( {EFG} \right)\\G \in BD \subset \left( {BCD} \right),G \in FG \subset \left( {EFG} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (EFG) và (BCD) là GH.

Vì \(\left\{ \begin{array}{l}E \in AB \subset \left( {ABD} \right),E \in FE \subset \left( {EFG} \right)\\G \in BD \subset \left( {ABD} \right),G \in FG \subset \left( {EFG} \right)\end{array} \right.\) nên giao tuyến của hai mặt phẳng (EFG) và (ABD) là GE.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 4 trang 112 sách bài tập toán 11 - Chân trời sáng tạo tập 1 – hành trang không thể thiếu trong chuyên mục Sách bài tập Toán 11 trên nền tảng môn toán. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 4 trang 112 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1: Tổng quan và Phương pháp giải

Bài 4 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm. Bài tập này thường tập trung vào việc tìm cực trị của hàm số, một chủ đề quan trọng trong chương trình Toán học lớp 11. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:

Định nghĩa đạo hàm: Hiểu rõ khái niệm đạo hàm của hàm số tại một điểm và đạo hàm của hàm số.
Quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của các hàm số cơ bản (hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit) và quy tắc tính đạo hàm của hàm hợp.
Điều kiện cực trị: Hiểu rõ điều kiện cần và đủ để một điểm là điểm cực trị của hàm số.
Cách xác định điểm cực trị: Biết cách tìm đạo hàm bậc nhất và đạo hàm bậc hai của hàm số, sau đó sử dụng các điều kiện cực trị để xác định điểm cực trị.

Lời giải chi tiết bài 4 trang 112 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1

Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài tập. Giả sử bài tập yêu cầu tìm cực trị của hàm số f(x) = x³ - 3x² + 2. Dưới đây là các bước giải:

Tính đạo hàm bậc nhất: f'(x) = 3x² - 6x
Tìm điểm dừng: Giải phương trình f'(x) = 0 để tìm các điểm dừng: 3x² - 6x = 0 => x = 0 hoặc x = 2
Tính đạo hàm bậc hai: f''(x) = 6x - 6
Kiểm tra điều kiện cực trị:
- Tại x = 0: f''(0) = -6 < 0 => Hàm số đạt cực đại tại x = 0. Giá trị cực đại là f(0) = 2.
- Tại x = 2: f''(2) = 6 > 0 => Hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là f(2) = -2.

Vậy, hàm số f(x) = x³ - 3x² + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.

Các dạng bài tập tương tự và phương pháp giải

Ngoài bài tập tìm cực trị của hàm số bậc ba như ví dụ trên, còn có nhiều dạng bài tập tương tự khác, ví dụ:

Tìm cực trị của hàm số bậc bốn.
Tìm cực trị của hàm số lượng giác.
Tìm cực trị của hàm số mũ và logarit.

Phương pháp giải các bài tập này tương tự như ví dụ trên, chỉ khác ở việc hàm số có dạng phức tạp hơn, đòi hỏi học sinh phải vận dụng linh hoạt các quy tắc tính đạo hàm và điều kiện cực trị.

Lưu ý khi giải bài tập về cực trị hàm số

Để giải bài tập về cực trị hàm số một cách chính xác và hiệu quả, học sinh cần lưu ý những điều sau:

Kiểm tra kỹ điều kiện xác định của hàm số.
Tính đạo hàm chính xác.
Giải phương trình đạo hàm bậc nhất một cách cẩn thận.
Kiểm tra điều kiện cực trị bằng đạo hàm bậc hai hoặc phương pháp xét dấu đạo hàm bậc nhất.
Kết luận đúng về điểm cực trị và giá trị cực trị.

Giaitoan.edu.vn: Nguồn học Toán 11 uy tín và hiệu quả

Giaitoan.edu.vn là một website học Toán online uy tín, cung cấp đầy đủ các tài liệu học tập, bài giảng, bài tập và lời giải chi tiết cho các môn Toán từ lớp 6 đến lớp 12. Với đội ngũ giáo viên giàu kinh nghiệm và phương pháp giảng dạy hiện đại, Giaitoan.edu.vn cam kết giúp học sinh học Toán hiệu quả và đạt kết quả cao.