Bài 2 trang 121 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân. Bài tập này thường yêu cầu học sinh vận dụng các công thức và tính chất đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2 trang 121 sách bài tập Toán 11 Chân trời sáng tạo tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’. a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE). b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho \(AM = \frac{1}{3}AF,\) \(AN = \frac{1}{3}AD\). Chứng minh MN//(DCEF).
Đề bài
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’.
a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE).
b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho \(AM = \frac{1}{3}AF,\) \(AN = \frac{1}{3}AD\). Chứng minh MN//(DCEF).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).
Lời giải chi tiết
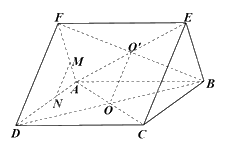
a) Vì O, O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O là trung điểm của BD, AC và O’ là trung điểm của BF, AE.
Vì O là trung điểm của BD, O’ là trung điểm của BF nên OO’ là đường trung bình của tam giác BDF. Do đó, OO’//DF (1)
Vì O là trung điểm của AC, O’ là trung điểm của AE nên OO’ là đường trung bình của tam giác ACE. Do đó, OO’//CE (2)
Từ (1) và (2) ta có: OO’//DF//CE
Vì OO’//DF, OO’ không nằm trên mặt phẳng (ADF) và \(DF \subset \left( {ADF} \right)\) nên OO’//(ADF).
Vì OO’//CE, OO’ không nằm trên mặt phẳng (BCE) và \(CE \subset \left( {BCE} \right)\) nên OO’//(BCE).
b) Vì \(AM = \frac{1}{3}AF,AN = \frac{1}{3}AD \Rightarrow \frac{{AM}}{{AF}} = \frac{{AN}}{{AD}} = \frac{1}{3}\)
Tam giác ADF có: \(\frac{{AM}}{{AF}} = \frac{{AN}}{{AD}} = \frac{1}{3}\) nên MN//DF (định lí Thalès đảo)
Vì MN//DF, MN không nằm trên mặt phẳng (DCEF) và \(DF \subset \left( {DCEF} \right)\) nên MN//(DCEF).
Bài 2 trong sách bài tập Toán 11 Chân trời sáng tạo tập 1 tập trung vào việc ứng dụng kiến thức về dãy số, đặc biệt là cấp số cộng và cấp số nhân, vào các bài toán thực tế. Nội dung bài tập thường yêu cầu học sinh xác định các yếu tố của dãy số (số hạng đầu, công sai/công bội), tính tổng của các số hạng trong dãy, hoặc tìm số hạng tổng quát của dãy.
Bài 2 trang 121 thường bao gồm các dạng bài tập sau:
(Giả sử bài 2 là một bài toán cụ thể về cấp số cộng. Nội dung sau đây là ví dụ minh họa, cần thay thế bằng lời giải chính xác của bài 2)
Bài toán: Cho cấp số cộng có số hạng đầu u1 = 2 và công sai d = 3. Tính tổng của 10 số hạng đầu tiên của cấp số cộng này.
Lời giải:
Áp dụng công thức tính tổng của cấp số cộng:
Sn = n/2 * (2u1 + (n-1)d)
Với n = 10, u1 = 2, d = 3, ta có:
S10 = 10/2 * (2*2 + (10-1)*3) = 5 * (4 + 27) = 5 * 31 = 155
Vậy, tổng của 10 số hạng đầu tiên của cấp số cộng là 155.
Ngoài sách giáo khoa và sách bài tập, bạn có thể tham khảo thêm các tài liệu sau:
Bài 2 trang 121 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về dãy số. Bằng cách nắm vững các công thức và kỹ năng giải bài tập, các em học sinh có thể tự tin giải quyết các bài toán tương tự và đạt kết quả tốt trong môn Toán.