Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 5 trang 100 sách bài tập Toán 11 Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp cho bạn các bước giải bài tập một cách rõ ràng, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất cho học sinh, sinh viên. Hãy cùng giaitoan.edu.vn khám phá lời giải bài tập này ngay nhé!
Một hộp chứa 10 quả bóng xanh và 10 quả bóng đỏ có kích thước và khối lượng như nhau. Lấy ra ngẫu nhiên đồng thời 5 quả bóng từ hộp. Sử dụng sơ đồ hình cây, tính xác suất của biến cố “Có ít nhất 3 quả bóng xanh trong 5 quả bóng lấy ra”.
Đề bài
Một hộp chứa 10 quả bóng xanh và 10 quả bóng đỏ có kích thước và khối lượng như nhau. Lấy ra ngẫu nhiên đồng thời 5 quả bóng từ hộp. Sử dụng sơ đồ hình cây, tính xác suất của biến cố “Có ít nhất 3 quả bóng xanh trong 5 quả bóng lấy ra”.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về sơ đồ hình cây để tính xác suất.
Lời giải chi tiết
Sơ đồ hình cây:
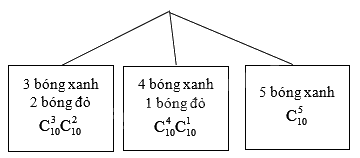
Xác suất của biến cố “Có ít nhất 3 quả bóng xanh trong 5 quả bóng lấy ra” là:
\(\frac{{C_{10}^3C_{10}^2 + C_{10}^4C_{10}^1 + C_{10}^5}}{{C_{20}^5}} = \frac{1}{2}\)
Bài 5 trang 100 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về đạo hàm, các quy tắc tính đạo hàm và các ứng dụng của đạo hàm.
Bài 5 trang 100 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. Lưu ý rằng, đây chỉ là một trong nhiều cách giải bài tập, học sinh có thể tìm tòi và khám phá các phương pháp giải khác nhau để nâng cao khả năng tư duy và giải quyết vấn đề.
Để tính đạo hàm của hàm số tại một điểm, ta sử dụng công thức:
f'(x0) = limh→0 (f(x0 + h) - f(x0)) / h
Trong đó:
Ví dụ, để tính đạo hàm của hàm số f(x) = x2 tại điểm x = 2, ta thực hiện như sau:
f'(2) = limh→0 ((2 + h)2 - 22) / h = limh→0 (4 + 4h + h2 - 4) / h = limh→0 (4h + h2) / h = limh→0 (4 + h) = 4
Vậy, đạo hàm của hàm số f(x) = x2 tại điểm x = 2 là 4.
Để tìm đạo hàm của hàm số, ta sử dụng các quy tắc tính đạo hàm đã học. Ví dụ:
Ví dụ, để tìm đạo hàm của hàm số f(x) = 3x2 + 2x - 1, ta thực hiện như sau:
f'(x) = 3 * 2x2-1 + 2 * 1 - 0 = 6x + 2
Vậy, đạo hàm của hàm số f(x) = 3x2 + 2x - 1 là 6x + 2.
Đạo hàm có nhiều ứng dụng trong thực tế, ví dụ như:
Ví dụ, để tìm cực trị của hàm số f(x) = x3 - 3x2 + 2, ta thực hiện như sau:
Kết quả, hàm số f(x) = x3 - 3x2 + 2 có cực đại tại x = 0 và cực tiểu tại x = 2.
Bài 5 trang 100 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và rèn luyện kỹ năng giải toán. Hy vọng rằng, với lời giải chi tiết và các ví dụ minh họa, học sinh sẽ hiểu rõ hơn về cách giải bài tập này và tự tin hơn trong quá trình học tập.