Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trắc nghiệm Toán 11 Chân trời sáng tạo tập 1. Chúng tôi hiểu rằng việc tự học và làm bài tập là rất quan trọng để nắm vững kiến thức.
Trang 160 sách bài tập Toán 11 Chân trời sáng tạo tập 1 chứa đựng những câu hỏi trắc nghiệm giúp bạn rèn luyện kỹ năng và củng cố lý thuyết đã học.
Hãy cùng giaitoan.edu.vn khám phá lời giải chi tiết cho từng câu hỏi để đạt kết quả tốt nhất!
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây. Tổng số học sinh tham gia kì thi đánh giá năng lực trên là A. 780. B. 787. C. 696. D. 697.
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.
Tổng số học sinh tham gia kì thi đánh giá năng lực trên là
A. 780.
B. 787.
C. 696.
D. 697.
Phương pháp giải:
Để tính tổng số học sinh tham gia kì thi, đếm xem mỗi khoảng điểm có bao nhiêu học sinh tham gia, rồi cộng tổng lại.
Lời giải chi tiết:
Tổng số học sinh tham gia kì thi đánh giá năng lực là:
\(1 + 8 + 24 + 54 + 95 + 95 + 133 + 122 + 104 + 62 + 55 + 21 + 12 + 1 = 787\) (học sinh)
Chọn B
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.

Giá trị đại diện cho nhóm chứa mốt của mẫu số liệu ghép nhóm trên là
A. 625,5.
B. 675,5.
C. 725,5.
D. 775,5.
Phương pháp giải:
+ Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
+ Sử dụng kiến thức về nhóm chứa một của mẫu số liệu để tính: Nhóm chứa mốt của mẫu số liệu ghép nhóm là nhóm có tần số lớn nhất.
Lời giải chi tiết:
Bảng số liệu ghép nhóm hiệu chỉnh:
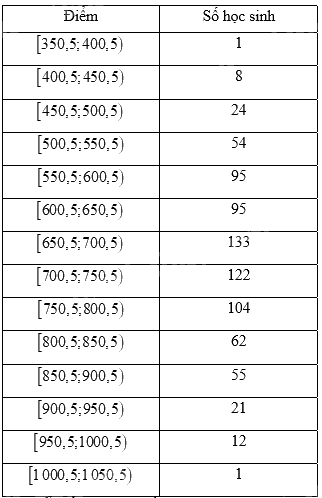
Nhóm chứa mốt của mẫu số liệu ghép nhóm là \(\left[ {650,5;700,5} \right)\).
Giá trị đại diện của nhóm \(\left[ {650,5;700,5} \right)\) là: \(\frac{1}{2}\left( {650,5 + 700,5} \right) = 675,5\)
Chọn B.
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.

Giá trị đại diện cho nhóm chứa trung vị của mẫu số liệu ghép nhóm trên là
A. 625,5.
B. 675,5.
C. 725,5.
D. 775,5.
Phương pháp giải:
+ Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
+ Để tìm nhóm chứa trung vị, ta đi tìm trung vị của mẫu số liệu rồi xét xem trung vị đó thuộc nhóm nào của bảng số liệu.
Lời giải chi tiết:
Bảng số liệu ghép nhóm hiệu chỉnh:

Gọi \({x_1},{x_2},...,{x_{787}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Vì \(n = 787\) nên trung vị của mẫu số liệu là \({x_{394}}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {650,5;700,5} \right)\).
Giá trị đại diện của nhóm \(\left[ {650,5;700,5} \right)\) là: \(\frac{1}{2}\left( {650,5 + 700,5} \right) = 675,5\)
Chọn B
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.

Giá trị đại diện cho nhóm chứa tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là
A. 625,5.
B. 675,5.
C. 725,5.
D. 775,5.
Phương pháp giải:
+ Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
+ Để tìm nhóm chứa tứ phân vị thứ nhất, ta đi tìm tứ phân vị thứ nhất rồi xét xem t tứ phân vị thứ nhất thuộc nhóm nào của bảng số liệu.
Lời giải chi tiết:
Bảng số liệu ghép nhóm hiệu chỉnh:

Gọi \({x_1},{x_2},...,{x_{787}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu là \({x_{197}}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {600,5;650,5} \right)\).
Giá trị đại diện của nhóm \(\left[ {600,5;650,5} \right)\) là: \(\frac{1}{2}\left( {600,5 + 650,5} \right) = 625,5\)
Chọn A
Trả lời các câu hỏi 1- 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.

Giá trị đại diện cho nhóm chứa tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là
A. 625,5.
B. 675,5.
C. 725,5.
D. 775,5.
Phương pháp giải:
+ Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
+ Để tìm nhóm chứa tứ phân vị thứ ba, ta đi tìm tứ phân vị thứ ba rồi xét xem tứ phân vị thứ ba thuộc nhóm nào của bảng số liệu.
Lời giải chi tiết:
Bảng số liệu ghép nhóm hiệu chỉnh:

Gọi \({x_1},{x_2},...,{x_{787}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Tứ phân vị thứ ba của mẫu số liệu là \({x_{591}}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {750,5;800,5} \right)\).
Giá trị đại diện của nhóm \(\left[ {750,5;800,5} \right)\) là: \(\frac{1}{2}\left( {750,5 + 800,5} \right) = 775,5\)
Chọn D
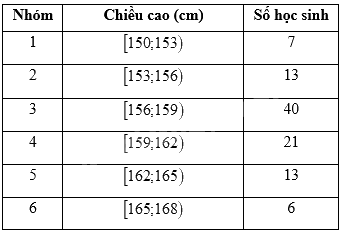
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

160,5 là giá trị đại diện cho nhóm
A. 2.
B. 3.
C. 4.
D. 5.
Phương pháp giải:
Sử dụng kiến thức về giá trị đại diện của mẫu số liệu ghép nhóm để tính: Giá trị chính giữa của mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm \(\left[ {{u_1};{u_2}} \right)\) có giá trị đại diện là \(\frac{1}{2}\left( {{u_1} + {u_2}} \right)\).
Lời giải chi tiết:
Giá trị đại diện của nhóm \(\left[ {159;162} \right)\) là: \(\frac{1}{2}\left( {159 + 162} \right) = 160,5\)
Vậy 160,5 là giá trị đại diện cho nhóm 4.
Chọn C
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Mốt của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A. 157,76.
B. 158,25.
C. 157,5.
D. 160,28.
Phương pháp giải:
Sử dụng kiến thức về mốt của mẫu số liệu để tính: Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_O}\) được xác định bởi công thức: \({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
Lời giải chi tiết:
Nhóm chứa mốt của mẫu số liệu là nhóm \(\left[ {156;159} \right)\).
Do đó, \({u_m} = 156,{n_{m - 1}} = 13,{n_m} = 40,{n_{m + 1}} = 21,{u_{m + 1}} = 159\)
Mốt của mẫu số liệu trên là:
\({M_O} = 156 + \frac{{40 - 13}}{{\left( {40 - 13} \right) + \left( {40 - 21} \right)}}.\left( {159 - 156} \right) \approx 157,76\)
Chọn A
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Trung vị của mẫu số liệu ghép nhóm trên là
A. 157,76.
B. 157,25.
C. 158,25.
D. 160,45.
Phương pháp giải:
Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính:
Gọi n là cỡ mẫu.
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị, \({n_m}\) là tần số của nhóm chứa trung vị,
\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, trung vị của mẫu số liệu là: \({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
Lời giải chi tiết:
Gọi \({x_1},{x_2},...,{x_{100}}\) là mẫu số liệu được xếp theo thứ tự không giảm
Do cỡ mẫu \(n = 100\) nên trung vị của mẫu số liệu là \(\frac{{{x_{50}} + {x_{51}}}}{2}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {156;159} \right)\).
Trung vị của mẫu số liệu ghép nhóm là: \({M_e} = 156 + \frac{{\frac{{100}}{2} - \left( {7 + 13} \right)}}{{40}}.\left( {159 - 156} \right) = 158,25\)
Chọn C
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A. 156,25.
B. 157,5.
C. 156,38.
D. 157,54.
Phương pháp giải:
Sử dụng kiến thức về xác định tứ phân vị của mẫu số liệu ghép nhóm để tính: Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất, \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất, \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
Lời giải chi tiết:
Gọi \({x_1},{x_2},...,{x_{100}}\) là mẫu số liệu được xếp theo thứ tự không giảm
Do cỡ mẫu \(n = 100\) nên tứ phân vị thứ nhất của mẫu số liệu là \(\frac{{{x_{25}} + {x_{26}}}}{2}\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {156;159} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 156 + \frac{{\frac{{100}}{4} - \left( {7 + 13} \right)}}{{40}}.\left( {159 - 156} \right) = 156,375 \approx 156,38\)
Chọn C
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A. 160,52.
B. 161,52.
C. 161,14.
D. 162,25.
Phương pháp giải:
Sử dụng kiến thức về tứ phân vị của mẫu số liệu ghép nhóm để tính: Để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu \({Q_3}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_j};{u_{j + 1}}} \right)\) chứa tứ phân vị thứ ba, \({n_j}\) là tần số của nhóm chứa tứ phân vị thứ ba, \(C = {n_1} + {n_2} + ... + {n_{j - 1}}\)
Khi đó, tứ phân vị thứ ba của mẫu số liệu là: \({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right)\)
Lời giải chi tiết:
Gọi \({x_1},{x_2},...,{x_{100}}\) là mẫu số liệu được xếp theo thứ tự không giảm
Do cỡ mẫu \(n = 100\) nên tứ phân vị thứ ba của mẫu số liệu là \(\frac{{{x_{75}} + {x_{76}}}}{2}\). Do đó tứ phân vị thứ ba của mẫu số liệu thuộc nhóm \(\left[ {159;162} \right)\).
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 159 + \frac{{\frac{{3.100}}{4} - \left( {7 + 13 + 40} \right)}}{{21}}.\left( {162 - 159} \right) \approx 161,14\)
Chọn C
Bài viết này cung cấp lời giải chi tiết cho các câu hỏi trắc nghiệm trang 160 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Chúng tôi sẽ phân tích từng câu hỏi, đưa ra phương pháp giải và đáp án chính xác, giúp bạn hiểu rõ bản chất của vấn đề và áp dụng vào các bài tập tương tự.
Chương trình Toán 11 Chân trời sáng tạo tập 1 tập trung vào các chủ đề như: Mệnh đề và tập hợp, Hàm số bậc nhất và bậc hai, Phương trình và bất phương trình bậc nhất và bậc hai, Hệ phương trình bậc nhất ba ẩn, và Vectơ trong mặt phẳng.
Các câu hỏi trắc nghiệm trang 160 thường xoay quanh các dạng bài sau:
Câu 1: (Đề bài câu hỏi trắc nghiệm)...
Lời giải:
...
Câu 2: (Đề bài câu hỏi trắc nghiệm)...
Lời giải:
...
...(Tiếp tục giải chi tiết cho tất cả các câu hỏi trắc nghiệm trên trang 160)
Kiến thức Toán 11 có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Để học Toán 11 hiệu quả hơn, bạn có thể tham khảo các tài liệu sau:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết các câu hỏi trắc nghiệm trang 160 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Chúc bạn học tập tốt và đạt kết quả cao!