Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn cách giải bài 5 trang 122 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi \(\left( \alpha \right)\) là mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA. Tìm giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp.
Đề bài
Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi \(\left( \alpha \right)\) là mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA. Tìm giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).
Lời giải chi tiết
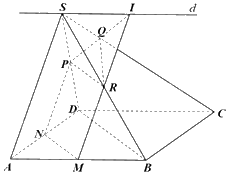
Gọi N, P, R lần lượt là trung điểm của AD, SD, SB.
Vì M, N lần lượt là trung điểm của AB, AD nên MN là đường trung bình của tam giác ABD. Do đó, MN//BD.
Vì P, R lần lượt là trung điểm của SD, SB nên PR là đường trung bình của tam giác SBD. Do đó, PR//BD.
Vì MN//BD, PR//BD nên MN//PR.
Suy ra bốn điểm M, N, P, R tạo thành mặt phẳng (MNPR).
Ta có: MN//BD, \(MN \subset \left( {MNPR} \right)\), BD không nằm trong mặt phẳng (MNPR) nên BD//(MNPR).
Chứng minh tương tự ta có: SA//(MNPR).
Vì mặt phẳng (MNPR) đi qua M và song song với BD, SA nên (MNPR) là mặt phẳng \(\left( \alpha \right)\).
Trong mặt phẳng (SAB), vẽ đường thẳng d đi qua S và d//AB//CD.
Khi đó, giả sử MR cắt d tại I, PI cắt SC tại Q. Suy ra, mặt phẳng \(\left( \alpha \right)\) là (MNPI).
Ta có: \(MN \subset \left( {ABCD} \right),MN \subset \left( {MNPI} \right)\) nên \(\left( {MNPI} \right) \cap \left( {ABCD} \right) = MN\) hay \(\left( \alpha \right) \cap \left( {ABCD} \right) = MN\).
Tương tự ta có:
\(\left( \alpha \right) \cap \left( {SAD} \right) = NP,\left( \alpha \right) \cap \left( {SCD} \right) = PQ,\left( \alpha \right) \cap \left( {SBC} \right) = QR,\left( \alpha \right) \cap \left( {ABS} \right) = MR\)
Bài 5 trang 122 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số lượng giác và đồ thị. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về các phép biến đổi lượng giác, tính chất của hàm số lượng giác và cách vẽ đồ thị hàm số để giải quyết.
Bài 5 thường bao gồm các dạng bài tập sau:
Để minh họa, chúng ta sẽ cùng giải một bài tập cụ thể. Giả sử bài tập yêu cầu:
“Tìm tập xác định của hàm số y = tan(2x + π/3)”
Lời giải:
Hàm số y = tan(2x + π/3) xác định khi và chỉ khi cos(2x + π/3) ≠ 0.
Điều này tương đương với:
2x + π/3 ≠ π/2 + kπ, với k ∈ Z
2x ≠ π/2 - π/3 + kπ, với k ∈ Z
2x ≠ π/6 + kπ, với k ∈ Z
x ≠ π/12 + kπ/2, với k ∈ Z
Vậy tập xác định của hàm số là: D = {x | x ≠ π/12 + kπ/2, k ∈ Z}
Để học tốt môn Toán 11, bạn có thể tham khảo các tài liệu sau:
Bài 5 trang 122 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số lượng giác. Hy vọng với hướng dẫn chi tiết và các lưu ý trên, bạn sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để tìm kiếm lời giải cho các bài tập khác và nâng cao kiến thức của bạn.