Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 6 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với \(AB = AC = a,\widehat {BAC} = {120^0}\),
Đề bài
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giáccân với \(AB = AC = a,\widehat {BAC} = {120^0}\), mặt phẳng (AB’C’) tạo với đáy một góc \({60^0}\). Tính thể tích V của khối lăng trụ đã cho.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng.
+ Sử dụng kiến thức về thể tích khối lăng trụ: Thể tích khối lăng trụ bằng diện tích đáy nhân với chiều cao: \(V = S.h\)
Lời giải chi tiết
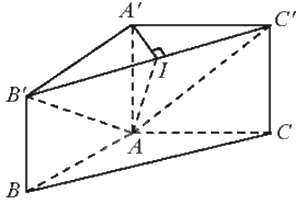
Kẻ \(A'I \bot B'C'\left( {I \in B'C'} \right)\). Vì \(AA' \bot \left( {A'B'C'} \right) \Rightarrow AA' \bot B'C'\)
Vì \(AA' \bot B'C',A'I \bot B'C' \Rightarrow B'C' \bot \left( {A'AI} \right) \Rightarrow B'C' \bot AI\)
Ta có: \(B'C' \bot AI,A'I \bot B'C',AI \subset \left( {AB'C'} \right),A'I \subset \left( {A'B'C'} \right)\) và B’C’ là giao tuyến của (AB’C’) và (A’B’C’). Do đó, \(\left( {\left( {AB'C'} \right),\left( {A'B'C'} \right)} \right) = \left( {A'I,AI} \right) = \widehat {A'IA} = {60^0}\)
Tam giác A’B’C’ cân tại A’ nên A’I là đường cao đồng thời là đường phân giác nên \(\widehat {B'A'I} = \frac{1}{2}\widehat {B'A'C'} = {60^0}\)
Tam giác B’A’I vuông tại I nên \(A'I = A'B'.\cos \widehat {B'A'I} = a.\cos {60^0} = \frac{1}{2}a\)
Vì \(AA' \bot \left( {A'B'C'} \right) \Rightarrow AA' \bot A'I\). Do đó, tam giác A’AI vuông tại A’.
Do đó, \(A'A = A'I.\tan \widehat {AIA'} = \frac{a}{2}.\tan {60^0} = \frac{{a\sqrt 3 }}{2}\)
Thể tích lăng trụ ABC.A’B’C’ là:
\({V_{ABC.A'B'C'}} \) \( = A'A.{S_{A'B'C'}} \) \( = \frac{1}{2}A'A.AB.AC\sin \widehat {BAC} \) \( = \frac{1}{2}\frac{{a\sqrt 3 }}{2}.a.a.\sin {120^0} \) \( = \frac{{3{a^2}}}{8}\)
Bài 6 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và công thức liên quan là rất quan trọng để hoàn thành bài tập này một cách chính xác.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giải bài 6 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2, bạn cần thực hiện theo các bước sau:
Ví dụ: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = 3x2 + 4x - 5
Để hiểu sâu hơn về đạo hàm, bạn có thể tham khảo thêm các tài liệu sau:
Bài 6 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, bạn sẽ tự tin hơn trong việc giải quyết bài tập này. Chúc bạn học tập tốt!
| Hàm số | Đạo hàm |
|---|---|
| f(x) = c (hằng số) | f'(x) = 0 |
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin x | f'(x) = cos x |
| f(x) = cos x | f'(x) = -sin x |