Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 8 trang 31 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các bạn. Hãy cùng theo dõi và luyện tập để nắm vững kiến thức Toán 11 nhé!
Theo định luật khúc xạ ánh sáng, khi một tia sáng được chiếu tới mặt phân cách giữa hai môi trường trong suốt không đồng chất thì tỉ số \(\frac{{\sin i}}{{\sin r}}\), với i là góc tới và r là góc khúc xạ, là một hằng số phụ thuộc vào chiết suất của hai môi trường.
Đề bài
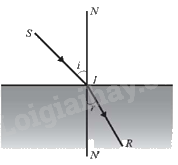
Theo định luật khúc xạ ánh sáng, khi một tia sáng được chiếu tới mặt phân cách giữa hai môi trường trong suốt không đồng chất thì tỉ số \(\frac{{\sin i}}{{\sin r}}\), với i là góc tới và r là góc khúc xạ, là một hằng số phụ thuộc vào chiết suất của hai môi trường. Biết rằng khi góc tới là \({45^o}\) thì góc khúc xạ bằng \({30^o}\). Khi góc tới là \({60^o}\) thì góc khúc xạ là bao nhiêu? Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về phương trình lượng giác cơ bản để giải: Phương trình \(\sin x = m\) có nghiệm khi \(\left| m \right| \le 1\). Khi đó, nghiệm của phương trình là \(x = \alpha + k2\pi \left( {k \in \mathbb{Z}} \right)\); \(x = \pi - \alpha + k2\pi \left( {k \in \mathbb{Z}} \right)\) với \(\alpha \) là góc thuộc \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\).
Lời giải chi tiết
Theo đầu bài ta có: \(\frac{{\sin {{45}^0}}}{{\sin {{30}^0}}} = \frac{{\sin {{60}^0}}}{{\sin r}} \) \( \Leftrightarrow \sin r = \frac{{\sin {{60}^0}.\sin {{30}^0}}}{{\sin {{45}^0}}} = \frac{{\sqrt 6 }}{4}\)
Suy ra: \(r \approx 37,{76^0}\)
Bài 8 trang 31 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số lượng giác và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép biến đổi lượng giác cơ bản, tính chất của hàm số lượng giác và kỹ năng vẽ đồ thị để giải quyết các bài toán cụ thể.
Bài 8 bao gồm các dạng bài tập sau:
Đề bài: Xác định tập xác định của hàm số y = tan(2x + π/3).
Lời giải: Hàm số y = tan(2x + π/3) xác định khi và chỉ khi 2x + π/3 ≠ π/2 + kπ, với k là số nguyên. Điều này tương đương với 2x ≠ π/6 + kπ, hay x ≠ π/12 + kπ/2, với k là số nguyên. Vậy tập xác định của hàm số là D = R \ {π/12 + kπ/2 | k ∈ Z}.
Đề bài: Tìm tập giá trị của hàm số y = 2sin(x) + 1.
Lời giải: Vì -1 ≤ sin(x) ≤ 1, với mọi x thuộc tập số thực, nên -2 ≤ 2sin(x) ≤ 2. Do đó, -1 ≤ 2sin(x) + 1 ≤ 3. Vậy tập giá trị của hàm số là [-1, 3].
Đề bài: Xét tính chẵn, lẻ của hàm số y = cos(x) + x2.
Lời giải: Ta có y(-x) = cos(-x) + (-x)2 = cos(x) + x2 = y(x). Vậy hàm số y = cos(x) + x2 là hàm số chẵn.
Để giải tốt các bài tập về hàm số lượng giác, học sinh cần nắm vững các kiến thức sau:
Để củng cố kiến thức và rèn luyện kỹ năng, các bạn có thể tự giải thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Ngoài ra, hãy tham khảo các tài liệu học tập trực tuyến và tìm kiếm sự giúp đỡ của giáo viên hoặc bạn bè khi gặp khó khăn.
Bài 8 trang 31 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số lượng giác và đồ thị. Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng mà chúng tôi cung cấp, các bạn sẽ tự tin hơn trong quá trình học tập và làm bài tập.