Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 8 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra và kỳ thi.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 8 trang 68 một cách cẩn thận, chi tiết, kèm theo các bước giải rõ ràng và dễ theo dõi.
Một hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước 2cm, 3cm và 6cm. Tính thể tích của khối tứ diện ACB’D’.
Đề bài
Một hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước 2cm, 3cm và 6cm. Tính thể tích của khối tứ diện ACB’D’.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về thể tích khối tứ diện để tính.
Lời giải chi tiết
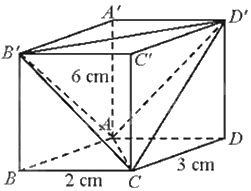
Ta có: \({{V}_{ABCD.ABCD}}\) \( ={{V}_{BAB'C}}+{{V}_{DACD'}}+{{V}_{A'B'AD'}}+{{V}_{C'B'CD'}}+{{V}_{ACB'D'}}\) \( =4{{V}_{BAB'C}}+{{V}_{ACB'D'}}\)
\(\Rightarrow {{V}_{ACB'D'}}\) \( ={{V}_{ABCD.ABCD}}-4{{V}_{BAB'C}}\) \( =\frac{1}{3}{{V}_{ABCD.ABCD}}\) \( =\frac{1}{3}.2.3.6\) \( =12\left( c{{m}^{3}} \right)\)
Bài 8 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của tổng, hiệu, tích, thương của các hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Phân tích bài toán:
Trước khi bắt tay vào giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Phân tích các dữ kiện đã cho và xác định các hàm số cần tính đạo hàm. Lập kế hoạch giải bài toán một cách logic và khoa học.
Giả sử bài 8 yêu cầu tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1. Để giải bài tập này, ta áp dụng quy tắc tính đạo hàm của tổng và hiệu của các hàm số:
f'(x) = (x3)' + (2x2)' - (5x)' + (1)'
Sử dụng quy tắc tính đạo hàm của hàm số lũy thừa, ta có:
(x3)' = 3x2
(2x2)' = 4x
(5x)' = 5
(1)' = 0
Vậy, f'(x) = 3x2 + 4x - 5
Bài 8 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thường xuất hiện các dạng bài tập sau:
Mẹo giải nhanh:
Để giải nhanh các bài tập về đạo hàm, học sinh nên ghi nhớ các công thức đạo hàm cơ bản và luyện tập thường xuyên. Sử dụng các quy tắc tính đạo hàm một cách linh hoạt và sáng tạo. Kiểm tra lại kết quả sau khi giải bài tập để đảm bảo tính chính xác.
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, học sinh nên làm thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác. Tham gia các diễn đàn học tập trực tuyến để trao đổi kinh nghiệm và học hỏi từ các bạn học.
Bài 8 trang 68 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm. Bằng cách nắm vững các kiến thức cơ bản, phân tích bài toán một cách logic và áp dụng các quy tắc tính đạo hàm một cách linh hoạt, học sinh có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc các bạn học tập tốt!