Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 4 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho khối chóp S.ABC có \(SA \bot \left( {ABC} \right)\), tam giác ABC có độ dài 3 cạnh là \(AB = 5a,BC = 8a,AC = 7a\), góc giữa SB và (ABC) là \({45^0}\). Tính thể tích khối chóp S.ABC.
Đề bài
Cho khối chóp S.ABC có \(SA \bot \left( {ABC} \right)\), tam giác ABC có độ dài 3 cạnh là \(AB = 5a,BC = 8a,AC = 7a\), góc giữa SB và (ABC) là \({45^0}\). Tính thể tích khối chóp S.ABC.
Phương pháp giải - Xem chi tiết
- Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính:
+ Nếu đường thẳng a vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a với (P) bằng \({90^0}\).
+ Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a và hình chiếu a’ của a trên (P) gọi là góc giữa đường thẳng a và (P).
- Sử dụng kiến thức về thể tích hình chóp: Thể tích hình chóp bằng một phần ba diện tích đáy nhân với chiều cao: \(V = \frac{1}{3}S.h\)
Lời giải chi tiết
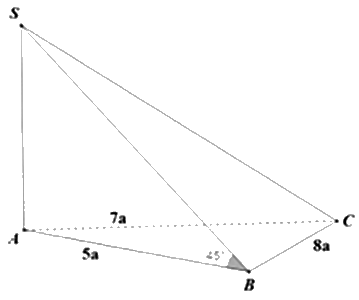
Vì \(SA \bot \left( {ABC} \right)\) nên A là hình chiếu của S trên mặt phẳng (ABC)
Ta có: \(\left( {SB,\left( {ABC} \right)} \right) = \left( {SB,AB} \right) = \widehat {SBA} = {45^0}\)
Vì \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AB\). Do đó, tam giác SAB vuông cân tại A.
Suy ra, \(SA = AB = 5a\).
Nửa chu vi tam giác ABC là: \(p = \frac{{5a + 7a + 8a}}{2} = 10a\)
Diện tích tam giác ABC là: \({S_{ABC}} = \sqrt {10a\left( {10a - 5a} \right)\left( {10a - 7a} \right)\left( {10a - 8a} \right)} = 10{a^2}\sqrt 3 \)
Thể tích khối chóp S. ABC là: \(V = \frac{1}{3}SA.{S_{ABC}} = \frac{1}{3}.5a.10{a^2}\sqrt 3 = \frac{{50{a^3}\sqrt 3 }}{3}\)
Bài 4 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể. Việc nắm vững kiến thức nền tảng và luyện tập thường xuyên là chìa khóa để giải quyết thành công bài tập này.
Bài 4 trang 76 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 4 trang 76, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. Lưu ý rằng, lời giải này chỉ mang tính chất tham khảo, bạn nên tự mình suy nghĩ và giải bài tập trước khi xem lời giải để rèn luyện kỹ năng giải toán.
Ví dụ: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1.
Lời giải:
f'(x) = d/dx (3x2 + 2x - 1) = 6x + 2
Ví dụ: Tính đạo hàm của hàm số g(x) = sin(x2).
Lời giải:
g'(x) = d/dx (sin(x2)) = cos(x2) * d/dx (x2) = cos(x2) * 2x = 2xcos(x2)
Ví dụ: Tìm các điểm cực trị của hàm số h(x) = x3 - 3x + 2.
Lời giải:
h'(x) = 3x2 - 3
Giải phương trình h'(x) = 0, ta được x = 1 hoặc x = -1.
Vậy hàm số h(x) có hai điểm cực trị tại x = 1 và x = -1.
Ví dụ: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số k(x) = x2 - 4x + 3 trên đoạn [0, 3].
Lời giải:
k'(x) = 2x - 4
Giải phương trình k'(x) = 0, ta được x = 2.
Tính giá trị của hàm số tại các điểm x = 0, x = 2, x = 3:
Vậy giá trị lớn nhất của hàm số k(x) trên đoạn [0, 3] là 3, đạt được tại x = 0, và giá trị nhỏ nhất là -1, đạt được tại x = 2.
Để giải bài tập đạo hàm hiệu quả, bạn nên:
Hy vọng rằng, với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn khi giải bài 4 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2. Chúc bạn học tập tốt!