Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn cách giải bài 12 trang 95 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài tập này một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng để giúp bạn nắm vững kiến thức.
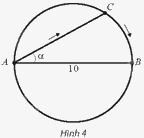
Tại một bể bơi có dạng hình tròn có đường kính \(AB = 10m\), một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc \(\alpha \left( {0 < \alpha < \frac{\pi }{2}} \right)\), rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi \(S\left( \alpha \right)\) là quãng đường người đó đã di chuyển. a) Viết công thức tính \(S\left( \alpha \right)\) theo \(\alpha \left( {0 < \alpha < \frac{\pi }{2}} \right)\). b) Xét tính liên tục của hàm số \(y = S\left( \alpha \right)\)
Đề bài
Tại một bể bơi có dạng hình tròn có đường kính \(AB = 10m\), một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc \(\alpha \left( {0 < \alpha < \frac{\pi }{2}} \right)\), rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi \(S\left( \alpha \right)\) là quãng đường người đó đã di chuyển.
a) Viết công thức tính \(S\left( \alpha \right)\) theo \(\alpha \left( {0 < \alpha < \frac{\pi }{2}} \right)\).
b) Xét tính liên tục của hàm số \(y = S\left( \alpha \right)\) trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\).
c) Tính các giới hạn \(\mathop {\lim }\limits_{\alpha \to {0^ + }} S\left( \alpha \right)\) và \(\mathop {\lim }\limits_{\alpha \to {{\frac{\pi }{2}}^ + }} S\left( \alpha \right)\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về các phép toán về giới hạn hữu hạn của hàm số để tính: Cho \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = L,\mathop {\lim }\limits_{x \to x_0^ + } g\left( x \right) = M\): \(\mathop {\lim }\limits_{x \to x_0^ + } \left[ {f\left( x \right) \pm g\left( x \right)} \right] = L \pm M\).
Lời giải chi tiết
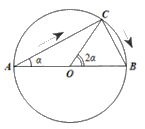
a) Kí hiệu O là tâm hình tròn.
Do tam giác ABC vuông tại C nên \(AC = AB\cos \alpha = 10\cos \alpha \left( m \right)\)
Ta có: \(\widehat {BOC} = 2\widehat {BAC} = 2\alpha \) nên độ dài cung BC là: \(l = OB.\widehat {BOC} = 5.2\alpha = 10\alpha \left( m \right)\)
Quãng đường di chuyển của người đó là:
\(S\left( \alpha \right) = AC + l = 10\cos \alpha + 10\alpha = 10\left( {\cos \alpha + \alpha } \right)\)(m) \(\left( {0 < \alpha < \frac{\pi }{2}} \right)\)
b) Do các hàm số \(y = \alpha ,y = \cos \alpha \) liên tục trên \(\mathbb{R}\) nên hàm số \(y = S\left( \alpha \right)\) liên tục trên \(\left( {0;\frac{\pi }{2}} \right)\).
c) \(\mathop {\lim }\limits_{\alpha \to {0^ + }} S\left( \alpha \right) = \mathop {\lim }\limits_{\alpha \to {0^ + }} 10\left( {\alpha + \cos \alpha } \right) = 10\left( {\mathop {\lim }\limits_{\alpha \to {0^ + }} \alpha + \mathop {\lim }\limits_{x \to {0^ + }} \cos \alpha } \right) = 10\left( {0 + 1} \right) = 10\)
\(\mathop {\lim }\limits_{\alpha \to {{\left( {\frac{\pi }{2}} \right)}^ + }} S\left( \alpha \right) = \mathop {\lim }\limits_{\alpha \to {{\left( {\frac{\pi }{2}} \right)}^ + }} 10\left( {\alpha + \cos \alpha } \right) = 10\left( {\mathop {\lim }\limits_{\alpha \to {{\left( {\frac{\pi }{2}} \right)}^ + }} \alpha + \mathop {\lim }\limits_{\alpha \to {{\left( {\frac{\pi }{2}} \right)}^ + }} \cos \alpha } \right) = 10\left( {\frac{\pi }{2} + 0} \right) = 5\pi \)
Bài 12 trang 95 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số lượng giác và đồ thị. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về tính chất của hàm số lượng giác, các phép biến đổi lượng giác và sử dụng đồ thị để giải quyết.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp bạn lựa chọn phương pháp giải phù hợp và tránh sai sót không đáng có.
Để giải bài 12 trang 95 sách bài tập Toán 11 - Chân trời sáng tạo tập 1, chúng ta cần thực hiện các bước sau:
Ví dụ minh họa: (Giả sử bài 12 yêu cầu tìm tập xác định của hàm số y = tan(2x + π/3)).
Để tìm tập xác định của hàm số y = tan(2x + π/3), ta cần giải điều kiện: 2x + π/3 ≠ π/2 + kπ (k ∈ Z).
Suy ra: 2x ≠ π/6 + kπ (k ∈ Z).
Vậy: x ≠ π/12 + kπ/2 (k ∈ Z).
Tập xác định của hàm số là: D = R \ {π/12 + kπ/2 | k ∈ Z}.
Ngoài bài 12 trang 95, sách bài tập Toán 11 - Chân trời sáng tạo tập 1 còn có nhiều bài tập tương tự về hàm số lượng giác. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, bạn cần nắm vững các kiến thức về:
Để học tốt môn Toán 11, đặc biệt là phần hàm số lượng giác, bạn nên:
Bài 12 trang 95 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số lượng giác. Hy vọng với hướng dẫn chi tiết này, bạn đã có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!