Bài 12 trang 85 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 12 trang 85 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Trong mặt phẳng tọa độ Oxy, cho điểm \(M\left( {t,{t^2}} \right),t > 0\), nằm trên đường parabol \(y = {x^2}\). Đường trung trực của đoạn thẳng OM cắt trục tung tại N. Điểm N dần đến điểm nào khi M dần đến điểm O?
Đề bài
Trong mặt phẳng tọa độ Oxy, cho điểm \(M\left( {t,{t^2}} \right),t > 0\), nằm trên đường parabol \(y = {x^2}\). Đường trung trực của đoạn thẳng OM cắt trục tung tại N. Điểm N dần đến điểm nào khi M dần đến điểm O?
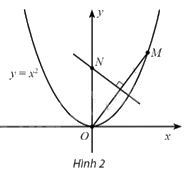
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về giới hạn một phía để tính:
+ Cho \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = L,\mathop {\lim }\limits_{x \to x_0^ + } g\left( x \right) = M\), khi đó: \(\mathop {\lim }\limits_{x \to x_0^ + } \left[ {f\left( x \right) + g\left( x \right)} \right] = L + M\)
+ \(\mathop {\lim }\limits_{x \to x_0^ + } c = c\) (với c là hằng số).
Lời giải chi tiết
Trung điểm của đoạn thẳng OM là \(I\left( {\frac{t}{2};\frac{{{t^2}}}{2}} \right)\)
Đường trung trực của OM nhận vectơ \(\overrightarrow {OM} = \left( {t,{t^2}} \right)\) làm vectơ pháp tuyến nên có phương trình d: \(t\left( {x - \frac{t}{2}} \right) + {t^2}\left( {y - \frac{{{t^2}}}{2}} \right) = 0\).
Thay \(x = 0\) vào phương trình của d, ta nhận được \(y = \frac{1}{2}\left( {1 + {t^2}} \right)\)
Suy ra \(N\left( {0;\frac{1}{2}\left( {1 + {t^2}} \right)} \right)\).
Điểm M dần đến điểm O khi t dần đến \({0^ + }\). Ta có: \(\mathop {\lim }\limits_{t \to {0^ + }} \frac{1}{2}\left( {1 + {t^2}} \right) = \frac{1}{2}\left( {1 + {0^2}} \right) = \frac{1}{2}\).
Suy ra điểm M dần đến điểm O khi điểm N dần đến điểm \(A\left( {0;\frac{1}{2}} \right)\).
Bài 12 trang 85 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1 thuộc chương trình học về đạo hàm của hàm số. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán liên quan đến tốc độ thay đổi, cực trị của hàm số.
Bài 12 thường bao gồm các dạng bài tập sau:
Để giải bài 12 trang 85 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1 hiệu quả, học sinh cần:
(Ở đây sẽ là lời giải chi tiết cho từng câu hỏi của bài 12. Ví dụ:)
Giải:
f'(x) = 3x^2 + 4x - 5
Giải:
g'(x) = 4x^3 - 8x
Giải phương trình g'(x) = 0, ta được x = 0, x = √2, x = -√2
Khảo sát dấu của g'(x) trên các khoảng xác định, ta thấy:
Vậy hàm số g(x) đạt cực đại tại x = -√2 và x = √2, đạt cực tiểu tại x = 0.
Để củng cố kiến thức về đạo hàm, học sinh có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 11 - Chân trời sáng tạo tập 1 và các tài liệu học tập khác.
Bài 12 trang 85 Sách bài tập Toán 11 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh hiểu sâu hơn về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán.