Bài 3 trang 161 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về tổ hợp và xác suất. Bài tập này thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 161, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Bảng sau thống kê doanh số bán hàng của các nhân viên một trung tâm thương mại trong một ngày. a) Hãy ước lượng số trung bình, mốt và trung vị của mẫu số liệu ghép nhóm trên. b) Trung tâm thương mại dự định sẽ thưởng cho 25% số nhân viên có doanh số bán hàng cao nhất. Theo mẫu số liệu trên, trung tâm thương mại nên khen thưởng các nhân viên có doanh số bán hàng ít nhất là bao nhiêu?
Đề bài
Bảng sau thống kê doanh số bán hàng của các nhân viên một trung tâm thương mại trong một ngày.

a) Hãy ước lượng số trung bình, mốt và trung vị của mẫu số liệu ghép nhóm trên.
b) Trung tâm thương mại dự định sẽ thưởng cho 25% số nhân viên có doanh số bán hàng cao nhất. Theo mẫu số liệu trên, trung tâm thương mại nên khen thưởng các nhân viên có doanh số bán hàng ít nhất là bao nhiêu?
Phương pháp giải - Xem chi tiết
a) + Sử dụng kiến thức về số trung bình của mẫu số liệu để tính:
Giả sử mẫu số được cho dưới dạng bảng tần số ghép nhóm:
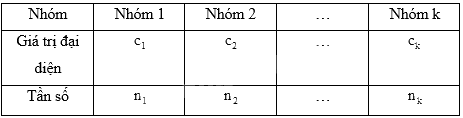
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).
+ Sử dụng kiến thức về mốt của mẫu số liệu để tính: Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_O}\) được xác định bởi công thức: \({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
+ Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính:
Gọi n là cỡ mẫu.
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị, \({n_m}\) là tần số của nhóm chứa trung vị,
\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khi đó, trung vị của mẫu số liệu là: \({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right)\).
+ Sử dụng kiến thức về xác định tứ phân vị của mẫu số liệu ghép nhóm để tính:
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm, kí hiệu \({Q_2}\), cũng chính là trung vị của mẫu số liệu ghép nhóm.
b) Để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu \({Q_3}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_j};{u_{j + 1}}} \right)\) chứa tứ phân vị thứ ba, \({n_j}\) là tần số của nhóm chứa tứ phân vị thứ ba, \(C = {n_1} + {n_2} + ... + {n_{j - 1}}\)
Khi đó, tứ phân vị thứ ba của mẫu số liệu là: \({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right)\)
Lời giải chi tiết
a) Ta có bảng số liệu bao gồm giá trị đại diện:
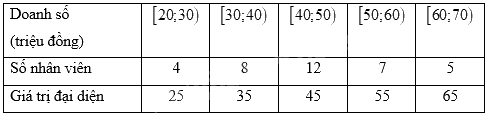
Cỡ mẫu \(n = 36\)
Số trung bình của mẫu số liệu là: \(\overline x = \frac{{25.4 + 35.8 + 45.12 + 55.7 + 65.5}}{{36}} = \frac{{815}}{{18}}\) (triệu đồng)
Nhóm chứa mốt của mẫu số liệu là \(\left[ {40;50} \right)\).
Do đó, \({u_m} = 40,{u_{m + 1}} = 50,{n_m} = 12,{n_{m + 1}} = 7,{u_{m + 1}} - {u_m} = 50 - 40 = 10\)
Mốt của mẫu số liệu là: \({M_O} = 40 + \frac{{12 - 8}}{{\left( {12 - 8} \right) + \left( {12 - 7} \right)}}.10 = \frac{{400}}{9}\) (triệu đồng)
Gọi \({x_1},{x_2},...,{x_{36}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có: \({x_1},...,{x_4} \in \left[ {20;30} \right),{x_5},...,{x_{12}} \in \left[ {30;40} \right),{x_{13}},...,{x_{24}} \in \left[ {40;50} \right),\)\({x_{25}},...,{x_{31}} \in \left[ {50;60} \right),{x_{32}},...,{x_{36}} \in \left[ {60;70} \right)\)
Do cỡ mẫu \(n = 36\) nên trung vị của mẫu số liệu là \(\frac{1}{2}\left( {{x_{18}} + {x_{19}}} \right)\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {40;50} \right)\).
Trung vị của mẫu số liệu ghép nhóm là: \({M_e} = 40 + \frac{{\frac{{36}}{2} - \left( {4 + 8} \right)}}{{12}}.\left( {50 - 40} \right) = 45\) (triệu đồng)
b) Do cỡ mẫu \(n = 36\) nên tứ phân vị thứ ba của mẫu số liệu là \(\frac{1}{2}\left( {{x_{27}} + {x_{28}}} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu thuộc nhóm \(\left[ {50;60} \right)\).
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 50 + \frac{{\frac{{3.36}}{4} - \left( {4 + 8 + 12} \right)}}{7}.\left( {60 - 50} \right) = \frac{{380}}{7}\) (triệu đồng)
Vậy trung tâm thương mại nên khen thưởng các nhân viên có doanh số một ngày ít nhất là \(\frac{{380}}{7}\) triệu đồng.
Bài 3 trong sách bài tập Toán 11 Chân trời sáng tạo tập 1 tập trung vào việc ứng dụng các kiến thức về hoán vị, chỉnh hợp và tổ hợp để giải quyết các bài toán đếm. Nắm vững các công thức và phương pháp giải là chìa khóa để hoàn thành bài tập này một cách hiệu quả.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết từng phần của bài 3:
...
...
...
Khi giải các bài tập về tổ hợp và xác suất, các em cần lưu ý những điều sau:
Ví dụ 1: Có bao nhiêu cách sắp xếp 5 cuốn sách khác nhau lên một kệ sách?
Lời giải: Đây là một bài toán về hoán vị. Số cách sắp xếp 5 cuốn sách khác nhau là 5! = 5 x 4 x 3 x 2 x 1 = 120 cách.
Ví dụ 2: Từ một nhóm 10 người, chọn ra 3 người để thành lập một tổ xung kích. Hỏi có bao nhiêu cách chọn?
Lời giải: Đây là một bài toán về tổ hợp. Số cách chọn 3 người từ 10 người là C(10, 3) = 10! / (3! x 7!) = (10 x 9 x 8) / (3 x 2 x 1) = 120 cách.
Bài 3 trang 161 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tổ hợp và xác suất. Bằng cách nắm vững các công thức và phương pháp giải, các em có thể tự tin giải quyết các bài toán tương tự.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh học tập tốt hơn. Chúc các em thành công!