Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 4 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các bạn. Hãy cùng theo dõi và luyện tập để nắm vững kiến thức Toán 11 nhé!
Cho hàm số \(y = \sin x\) với \(x \in \left[ { - 2\pi ;2\pi } \right]\). a) Vẽ đồ thị hàm số đã cho. b) Tìm các giá trị của \(x \in \left[ {\frac{{ - 5\pi }}{3};\frac{{7\pi }}{3}} \right]\) sao cho \(\sin \left( {\frac{\pi }{3} - x} \right) = - 1\).
Đề bài
Cho hàm số \(y = \sin x\) với \(x \in \left[ { - 2\pi ;2\pi } \right]\).
a) Vẽ đồ thị hàm số đã cho.
b) Tìm các giá trị của \(x \in \left[ {\frac{{ - 5\pi }}{3};\frac{{7\pi }}{3}} \right]\) sao cho \(\sin \left( {\frac{\pi }{3} - x} \right) = - 1\).
c) Tìm các giá trị của \(x \in \left[ {\frac{{ - 9\pi }}{8};\frac{{7\pi }}{8}} \right]\) sao cho \(\sin \left( {2x + \frac{\pi }{4}} \right) > 0\).
d) Tìm m để có bốn giá trị \(\alpha \in \left[ { - 2\pi ;2\pi } \right]\) phân biệt thỏa mãn \(\sin \alpha = m\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về đồ thị hàm số \(y = \sin x\) để giải.
Lời giải chi tiết
a) Ta có đồ thị hàm số \(y = \sin x\) với \(x \in \left[ { - 2\pi ;2\pi } \right]\):
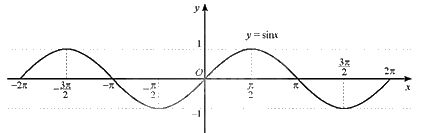
b) Đặt \(\frac{\pi }{3} - x = t\). Vì \(\frac{{ - 5\pi }}{3} \le x \le \frac{{7\pi }}{3} \Rightarrow - 2\pi \le t \le 2\pi \).
Từ đồ thị hàm số trong phần a, ta có: \(\sin t = - 1\) khi và chỉ khi \(t = \frac{{ - \pi }}{2}\) hoặc \(t = \frac{{3\pi }}{2}\)
Do đó, \(\frac{\pi }{3} - x = \frac{{ - \pi }}{2}\) hoặc \(\frac{\pi }{3} - x = \frac{{3\pi }}{2}\). Suy ra: \(x = \frac{{5\pi }}{6}\) hoặc \(x = \frac{{ - 7\pi }}{6}\)
c) Đặt \(2x + \frac{\pi }{4} = t\). Vì \(\frac{{ - 9\pi }}{8} \le x \le \frac{{7\pi }}{8} \Rightarrow - 2\pi \le t \le 2\pi \).
Từ đồ thị hàm số trong phần a, ta có: \(\sin t > 0\) khi và chỉ khi \( - 2\pi < t < - \pi \) hoặc \(0 < t < \pi \)
Suy ra: \( - 2\pi < 2x + \frac{\pi }{4} < - \pi \) hoặc \(0 < 2x + \frac{\pi }{4} < \pi \)
Do đó, \(\frac{{ - 9\pi }}{8} \le x \le \frac{{ - 5\pi }}{8}\) hoặc \(\frac{{ - \pi }}{8} \le x \le \frac{{3\pi }}{8}\)
d) Có bốn giá trị \(\alpha \in \left[ { - 2\pi ;2\pi } \right]\) phân biệt thỏa mãn \(\sin \alpha = m\) khi và chỉ khi đường thẳng \(y = m\) cắt đồ thị hàm số \(y = \sin \alpha \) tại bốn điểm. Từ đồ thị hàm số ở trên, điều này xảy ra khi và chỉ khi \( - 1 < m < 0\) hoặc \(0 < m < 1\).
Bài 4 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về parabol, đỉnh của parabol, trục đối xứng và các điểm đặc biệt của parabol để giải quyết các bài toán liên quan đến việc xác định phương trình parabol khi biết các yếu tố khác nhau.
Bài 4 bao gồm các câu hỏi nhỏ, mỗi câu hỏi tập trung vào một khía cạnh cụ thể của việc xác định phương trình parabol. Cụ thể:
Để giải bài 4 trang 27, học sinh cần nắm vững các công thức và phương pháp sau:
Ta có phương trình parabol có dạng: y = a(x - 1)2 + 2. Thay tọa độ điểm A(3; 6) vào phương trình, ta được:
6 = a(3 - 1)2 + 2
6 = 4a + 2
4a = 4
a = 1
Vậy phương trình parabol là: y = (x - 1)2 + 2 = x2 - 2x + 3
Tương tự như câu a, ta có phương trình parabol có dạng: y = a(x + 1)2 - 2. Thay tọa độ điểm B(0; -1) vào phương trình, ta được:
-1 = a(0 + 1)2 - 2
-1 = a - 2
a = 1
Vậy phương trình parabol là: y = (x + 1)2 - 2 = x2 + 2x - 1
Ta có phương trình parabol có dạng: y = a(x + 2)2 + k. Thay tọa độ điểm C(1; 3) và D(-5; 3) vào phương trình, ta được hệ phương trình:
3 = a(1 + 2)2 + k
3 = a(-5 + 2)2 + k
Giải hệ phương trình này, ta được a = 0 và k = 3. Tuy nhiên, a ≠ 0 nên có lẽ đề bài có sai sót. Nếu trục đối xứng là x = -2 và hai điểm C, D có cùng tung độ thì parabol là đường thẳng y = 3. Tuy nhiên, theo định nghĩa parabol thì a phải khác 0. Giả sử đề bài đúng, ta có thể tìm ra một parabol thỏa mãn điều kiện này.
3 = 9a + k
3 = 9a + k
Từ đây suy ra k = 3 - 9a. Thay vào phương trình y = a(x+2)^2 + k, ta có y = a(x+2)^2 + 3 - 9a.
Tương tự như câu c, ta có phương trình parabol có dạng: y = a(x - 3)2 + k. Thay tọa độ điểm E(1; -2) và F(5; -2) vào phương trình, ta được hệ phương trình:
-2 = a(1 - 3)2 + k
-2 = a(5 - 3)2 + k
Giải hệ phương trình này, ta được a = 0 và k = -2. Tương tự như câu c, nếu trục đối xứng là x = 3 và hai điểm E, F có cùng tung độ thì parabol là đường thẳng y = -2. Tuy nhiên, theo định nghĩa parabol thì a phải khác 0. Giả sử đề bài đúng, ta có thể tìm ra một parabol thỏa mãn điều kiện này.
-2 = 4a + k
-2 = 4a + k
Từ đây suy ra k = -2 - 4a. Thay vào phương trình y = a(x-3)^2 + k, ta có y = a(x-3)^2 - 2 - 4a.
Bài 4 trang 27 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về parabol và phương pháp xác định phương trình parabol. Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng trên đây, các bạn học sinh sẽ tự tin hơn khi giải các bài tập tương tự.