Bài 4 trang 122 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp bạn hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của hai cạnh AB và CD, P là trung điểm của SA. Chứng minh: a) MN song song với các mặt phẳng (SBC) và (SAD); b) SB song song với (MNP); c) SC song song với (MNP); d) Gọi \({G_1}\) và \({G_2}\) theo thứ tự là trọng tâm của hai tam giác ABC và SBC. Chứng minh \({G_1}{G_2}\) song song với (SAD).
Đề bài
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của hai cạnh AB và CD, P là trung điểm của SA. Chứng minh:
a) MN song song với các mặt phẳng (SBC) và (SAD);
b) SB song song với (MNP);
c) SC song song với (MNP);
d) Gọi \({G_1}\) và \({G_2}\) theo thứ tự là trọng tâm của hai tam giác ABC và SBC. Chứng minh \({G_1}{G_2}\) song song với (SAD).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).
Lời giải chi tiết
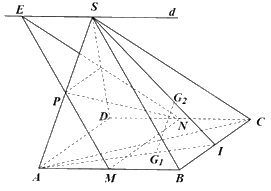
a) Hình bình hành ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD nên MN//AD//BC.
Ta có: MN//BC, \(BC \subset \left( {SBC} \right)\) và MN không nằm trong mặt phẳng (SBC) nên MN// (SBC).
Lại có: MN//AD, \(AD \subset \left( {SAD} \right)\) và MN không nằm trong mặt phẳng (SAD) nên MN// (SAD).
b) Vì P, M lần lượt là trung điểm của SA, AB nên PM là đường trung bình của tam giác SAB. Do đó, PM//SB. Mà \(PM \subset \left( {MNP} \right)\), SB không nằm trong mặt phẳng (MNP) nên SB//(MNP).
c) Trong mặt phẳng (SAB), vẽ đường thẳng d đi qua S và song song với AB.
Gọi E là giao điểm của MP và d.
Ta có: ES//AB, mà AB//CD nên ES//DC hay ES//NC (1)
Vì ES//MB, EM//SB nên tứ giác MBSE là hình bình hành, suy ra \(ES = MB\)
Mà \(MB = NC\) (vì M, N lần lượt là trung điểm của AB, DC và \(AB = DC\)), suy ra: \(ES = NC\) (2)
Từ (1) và (2) suy ra tứ giác ESCN là hình bình hành nên SC//NE.
Mà \(NE \subset \left( {MNP} \right)\), SC không nằm trong mặt phẳng (MNP) nên SC//(MNP).
d) Gọi I là trung điểm của BC.
Vì \({G_1}\) và \({G_2}\) lần lượt là trọng tâm của hai tam giác ABC và SBC nên \(\frac{{I{G_1}}}{{IA}} = \frac{{I{G_2}}}{{IS}} = \frac{1}{3}\).
Tam giác SIA có: \(\frac{{I{G_1}}}{{IA}} = \frac{{I{G_2}}}{{IS}} = \frac{1}{3}\) nên \({G_1}{G_2}//SA\) (định lí Thalès đảo)
Mà \(SA \subset \left( {SAD} \right)\), \({G_1}{G_2}\) không nằm trong mặt phẳng (SAD) nên \({G_1}{G_2}//\left( {SAD} \right)\).
Bài 4 trong sách bài tập Toán 11 Chân trời sáng tạo tập 1 tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến sự biến thiên của hàm số. Cụ thể, bài toán yêu cầu học sinh tìm đạo hàm, xét dấu đạo hàm và xác định các khoảng đơn điệu của hàm số. Việc nắm vững các khái niệm và kỹ năng này là nền tảng quan trọng để học tốt các chương trình Toán học nâng cao hơn.
Bài 4 trang 122 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thường có dạng như sau: Cho hàm số y = f(x). Hãy tìm đạo hàm f'(x), xét dấu f'(x) và xác định các khoảng đơn điệu của hàm số.
Để giải bài toán này, học sinh cần thực hiện các bước sau:
Để cung cấp lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài toán. Giả sử bài toán có dạng như sau:
Bài toán: Cho hàm số y = x3 - 3x2 + 2. Hãy tìm đạo hàm, xét dấu đạo hàm và xác định các khoảng đơn điệu của hàm số.
Lời giải:
Xét dấu y' trên các khoảng:
| Khoảng | x | y' | Kết luận |
|---|---|---|---|
| (-∞; 0) | -1 | 3(-1)2 - 6(-1) = 9 > 0 | Hàm số đồng biến |
| (0; 2) | 1 | 3(1)2 - 6(1) = -3 < 0 | Hàm số nghịch biến |
| (2; +∞) | 3 | 3(3)2 - 6(3) = 9 > 0 | Hàm số đồng biến |
Việc giải bài 4 trang 122 sách bài tập Toán 11 Chân trời sáng tạo tập 1 không chỉ giúp học sinh nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm mà còn là cơ sở để giải quyết các bài toán phức tạp hơn trong chương trình Toán học. Ngoài ra, kiến thức này còn có ứng dụng trong nhiều lĩnh vực khác như vật lý, kinh tế, và kỹ thuật.
Bài 4 trang 122 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các bạn học sinh sẽ hiểu rõ hơn về bài toán và tự tin giải quyết các bài tập tương tự.