Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 2 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). a) Chứng minh hai mặt phẳng (ABE) và (DFK) cùng vuông góc với (ADC). b) Gọi O và H là trực tâm \(\Delta BCD\) và \(\Delta ACD\).
Đề bài
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). Vẽ các đường cao BE, DF của tam giác BCD, đường cao DK của tam giác ACD.
a) Chứng minh hai mặt phẳng (ABE) và (DFK) cùng vuông góc với (ADC).
b) Gọi O và H là trực tâm \(\Delta BCD\) và \(\Delta ACD\). Chứng minh OH vuông góc với (ADC).
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về điều kiện để hai mặt phẳng vuông góc: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
+ Sử dụng kiến thức về tính chất cơ bản của hai mặt phẳng vuông góc: Nếu hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng cũng vuông góc với mặt phẳng thứ ba.
Lời giải chi tiết
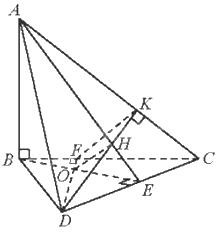
a) Vì AB là giao tuyến của hai mặt phẳng (ABC) và (ABD), hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC) nên \(AB \bot \left( {BCD} \right)\)\( \Rightarrow AB \bot CD\)
Mà \(BE \bot CD \Rightarrow CD \bot \left( {ABE} \right)\). Lại có: \(CD \subset \left( {ACD} \right) \Rightarrow \left( {ABE} \right) \bot \left( {ACD} \right)\)
Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot DF\), mà \(DF \bot BC \Rightarrow DF \bot \left( {ABC} \right) \Rightarrow DF \bot AC\)
Mà \(DK \bot AC \Rightarrow AC \bot \left( {DFK} \right)\). Lại có: \(AC \subset \left( {ADC} \right) \Rightarrow \left( {DFK} \right) \bot \left( {ADC} \right)\)
b) Vì O là giao điểm của hai đường cao BE và DF, H là giao điểm của hai đường cao AE và DK nên OH là giao tuyến của (ABE) và (DFK).
Mà \(\left( {ABE} \right) \bot \left( {ACD} \right),\left( {DFK} \right) \bot \left( {ADC} \right)\) và nên \(OH \bot \left( {ACD} \right)\)
Bài 2 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể. Việc nắm vững lý thuyết và kỹ năng tính toán là yếu tố then chốt để hoàn thành bài tập này một cách chính xác.
Bài 2 thường bao gồm các dạng bài tập sau:
Để giải bài 2 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2, bạn cần thực hiện theo các bước sau:
Ví dụ: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1.
Giải:
Áp dụng quy tắc tính đạo hàm của tổng và tích, ta có:
f'(x) = d(3x2)/dx + d(2x)/dx - d(1)/dx
f'(x) = 6x + 2 - 0
f'(x) = 6x + 2
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài 2 trang 76 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm. Hy vọng với hướng dẫn chi tiết và các mẹo giải bài tập hiệu quả trên đây, bạn sẽ tự tin hơn trong việc giải quyết bài tập này và đạt kết quả tốt trong các kỳ thi.