Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 6 trang 62 sách bài tập Toán 11 - Chân trời sáng tạo tập 2. Bài viết này cung cấp phương pháp giải bài tập một cách rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ quá trình học tập của bạn. Hãy cùng theo dõi và tham khảo lời giải chi tiết dưới đây!
Người ta cần sơn tất cả các mặt của một khối bê tông hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 2m, đáy nhỏ có cạnh bằng 1m và cạnh bên bằng 2m (Hình 14). Tính tổng diện tích các bề mặt cần sơn.
Đề bài
Người ta cần sơn tất cả các mặt của một khối bê tông hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 2m, đáy nhỏ có cạnh bằng 1m và cạnh bên bằng 2m (Hình 14). Tính tổng diện tích các bề mặt cần sơn.

Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về diện tích toàn phần của hình chóp cụt tứ giác đều: \(S = {S_{MB}} + {S_{ĐL}} + {S_{ĐN}}\) (MB: mặt bên, ĐL: đáy lớn, ĐN: đáy nhỏ)
Lời giải chi tiết
Diện tích đáy lớn là: \({S_{ĐL}} = {2^2} = 4\left( {{m^2}} \right)\)
Diện tích đáy nhỏ là: \({S_{ĐN}} = {1^2} = 1\left( {{m^2}} \right)\)
Giả sử các mặt bên được đặt tên và có dạng như hình vẽ dưới đây:
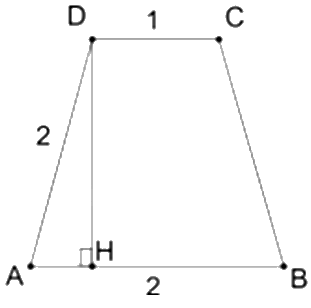
Tính được \(AH = \frac{1}{2}m\). Áp dụng định lí Pythagore vào tam giác AHD vuông tại H có:
\(DH = \sqrt {A{D^2} - A{H^2}} = \sqrt {{2^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt {15} }}{2}\left( m \right)\)
Tổng diện tích các mặt bên là:
\({S_{MB}} = 4{S_{ABCD}} = 4.\frac{1}{2}\left( {AB + CD} \right).DH = 3\sqrt {15} \left( {{m^2}} \right)\)
Tổng diện tích các mặt cần sơn là:
\(S = {S_{MB}} + {S_{ĐL}} + {S_{ĐN}} = 3\sqrt {15} + 4 + 1 = 3\sqrt {15} + 5\left( {{m^2}} \right)\)
Bài 6 trang 62 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 thuộc chương trình học về phép biến hình. Bài tập này tập trung vào việc vận dụng các kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán thực tế. Việc nắm vững các khái niệm và tính chất của các phép biến hình là vô cùng quan trọng để giải quyết bài tập này một cách hiệu quả.
Bài 6 trang 62 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 6 trang 62 sách bài tập Toán 11 - Chân trời sáng tạo tập 2, chúng tôi xin trình bày lời giải chi tiết cho từng phần của bài tập:
Để xác định ảnh của điểm A(1; 2) qua phép tịnh tiến theo vectơ v = (3; -1), ta sử dụng công thức:
A'(x'; y') = A(x; y) + v(a; b) = (x + a; y + b)
Trong trường hợp này, ta có:
A'(x'; y') = (1 + 3; 2 - 1) = (4; 1)
Vậy, ảnh của điểm A(1; 2) qua phép tịnh tiến theo vectơ v = (3; -1) là A'(4; 1).
Để tìm ảnh của điểm B(2; 0) qua phép quay tâm O(0; 0) góc -90°, ta sử dụng công thức:
B'(x'; y') = x cos α - y sin α; x sin α + y cos α
Trong trường hợp này, ta có α = -90° và B(x; y) = (2; 0). Do đó:
B'(x'; y') = 2 cos(-90°) - 0 sin(-90°); 2 sin(-90°) + 0 cos(-90°)
B'(x'; y') = 2 * 0 - 0 * (-1); 2 * (-1) + 0 * 0
B'(x'; y') = (0; -2)
Vậy, ảnh của điểm B(2; 0) qua phép quay tâm O(0; 0) góc -90° là B'(0; -2).
Để chứng minh hai tam giác ABC và A'B'C' đối xứng nhau qua đường thẳng d, ta cần chứng minh rằng:
Việc chứng minh này đòi hỏi phải sử dụng các tính chất của phép đối xứng trục và các định lý về tam giác.
Bài 6 trang 62 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về phép biến hình. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà chúng tôi đã cung cấp, các em học sinh sẽ tự tin hơn trong việc giải quyết bài tập này và đạt kết quả tốt trong môn Toán.