Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 11 trang 76 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài giải chi tiết dưới đây!
Tam giác \(O{A_1}{A_2}\) vuông cân tại \({A_2}\) có cạnh huyền \(O{A_1}\) bằng a. Bên ngoài tam giác \(O{A_1}{A_2}\), vẽ tam giác \(O{A_2}{A_3}\) vuông cân tại \({A_3}\). Tiếp theo, bên ngoài tam giác \(O{A_2}{A_3}\), vẽ tam giác \(O{A_3}{A_4}\) vuông cân tại \({A_4}\). Cứ tiếp tục quá trình như trên, ta vẽ được một dãy các hình tam giác vuông cân (Hình 2). Tính độ dài đường gấp khúc \({A_1}{A_2}{A_3}{A_4}...\)
Đề bài
Tam giác \(O{A_1}{A_2}\) vuông cân tại \({A_2}\) có cạnh huyền \(O{A_1}\) bằng a. Bên ngoài tam giác \(O{A_1}{A_2}\), vẽ tam giác \(O{A_2}{A_3}\) vuông cân tại \({A_3}\). Tiếp theo, bên ngoài tam giác \(O{A_2}{A_3}\), vẽ tam giác \(O{A_3}{A_4}\) vuông cân tại \({A_4}\). Cứ tiếp tục quá trình như trên, ta vẽ được một dãy các hình tam giác vuông cân (Hình 2). Tính độ dài đường gấp khúc \({A_1}{A_2}{A_3}{A_4}...\)
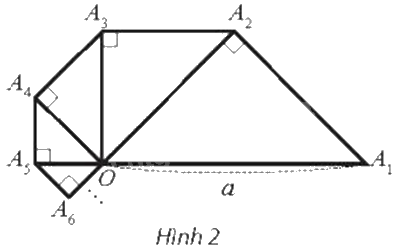
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tổng của cấp số nhân lùi vô hạn để tính độ dài đường gấp khúc: Cấp số nhân vô hạn \(\left( {{u_n}} \right)\) có công bội q thỏa mãn \(\left| q \right| < 1\) được gọi là cấp số nhân lùi vô hạn. Cấp số nhân lùi vô hạn này có tổng là: \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\)
Lời giải chi tiết
Ta có các góc \(\widehat {{A_1}O{A_2}},\widehat {{A_2}O{A_3}},\widehat {{A_3}O{A_4}},...\) đều bằng \({45^0}\).
Lại có: \({A_1}{A_2} = O{A_2} = O{A_1}.\cos {45^0} = a\frac{{\sqrt 2 }}{2}\);
\({A_2}{A_3} = O{A_3} = O{A_2}.\cos {45^0} = a\frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} = a{\left( {\frac{{\sqrt 2 }}{2}} \right)^2}\);
\({A_3}{A_4} = O{A_4} = O{A_3}.\cos {45^0} = a{\left( {\frac{{\sqrt 2 }}{2}} \right)^2}.\frac{{\sqrt 2 }}{2} = a{\left( {\frac{{\sqrt 2 }}{2}} \right)^3}\);…
Vậy độ dài các đoạn thẳng \({A_1}{A_2},{A_2}{A_3},{A_3}{A_4}...\) tạo thành cấp số nhân lùi vô hạn với số hạng đầu bằng \(a\frac{{\sqrt 2 }}{2}\) và công bội bằng \(\frac{{\sqrt 2 }}{2}\). Do đó, độ dài đường gấp khúc \({A_1}{A_2}{A_3}{A_4}...\) là: \(l = \frac{{a\sqrt 2 }}{2}.\frac{1}{{1 - \frac{{\sqrt 2 }}{2}}} = \frac{{a\sqrt 2 }}{{2 - \sqrt 2 }} = \frac{{a\sqrt 2 }}{2}\left( {2 + \sqrt 2 } \right) = a\left( {1 + \sqrt 2 } \right)\)
Bài 11 trang 76 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc hai. Để giải bài này, học sinh cần nắm vững kiến thức về:
Nội dung bài 11: Bài tập này thường yêu cầu học sinh xác định các yếu tố của hàm số bậc hai (a, b, c), tìm đỉnh của parabol, vẽ đồ thị hàm số, hoặc giải các bài toán liên quan đến ứng dụng của hàm số bậc hai.
Để giải bài 11 trang 76 sách bài tập Toán 11 Chân trời sáng tạo tập 1, chúng ta sẽ thực hiện theo các bước sau:
Giả sử bài 11 yêu cầu giải hàm số y = x2 - 4x + 3.
Giải:
1. Hàm số: y = x2 - 4x + 3
2. Hệ số: a = 1, b = -4, c = 3
3. Tọa độ đỉnh:
Vậy đỉnh của parabol là (2, -1).
4. Trục đối xứng: x = 2
5. Giao điểm với trục hoành:
x2 - 4x + 3 = 0
Giải phương trình, ta được x1 = 1 và x2 = 3. Vậy parabol cắt trục hoành tại hai điểm (1, 0) và (3, 0).
6. Giao điểm với trục tung:
Cho x = 0, ta được y = 3. Vậy parabol cắt trục tung tại điểm (0, 3).
7. Vẽ đồ thị hàm số dựa trên các thông tin trên.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 11 trang 76 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Chúc các em học tập tốt!
| Hàm số | Đỉnh | Trục đối xứng |
|---|---|---|
| y = x2 - 4x + 3 | (2, -1) | x = 2 |