Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 6 trang 13 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2. Bài viết này cung cấp đáp án đầy đủ, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật nhanh chóng nhất để hỗ trợ tối đa cho quá trình học tập của bạn.
Sử dụng máy tính cầm tay, tính (làm tròn đến chữ số thập phân thứ tư):
Đề bài
Sử dụng máy tính cầm tay, tính (làm tròn đến chữ số thập phân thứ tư):
a) \({\log _7}21\);
b) \(\log 2,25\);
c) \(\ln \sqrt {14} \);
d) \({\log _{0,5}}3 + {\log _5}0,3\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về máy tính bỏ túi để tính.
Lời giải chi tiết
a) Ta nhập vào máy tính:

Thu được kết quả
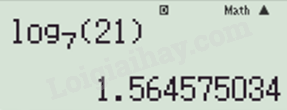
\({\log _7}21 \approx 1,5646\);
b) Ta nhập vào máy tính:

Thu được kết quả
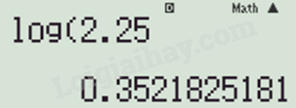
\(\log 2,25 \approx 0,3522\);
c) Ta nhập vào máy tính:

Thu được kết quả
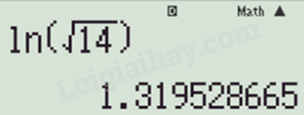
\(\ln \sqrt {14} \approx 1,3195\);
d) Ta nhập vào máy tính:

Thu được kết quả
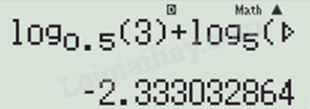
\({\log _{0,5}}3 + {\log _5}0,3 \approx - 2,3330\).
Bài 6 trang 13 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2 thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về phép biến hình affine để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh hiểu rõ định nghĩa, tính chất của phép biến hình affine, cũng như khả năng xác định các yếu tố của phép biến hình khi biết ảnh của một số điểm.
Bài 6 bao gồm các câu hỏi và bài tập khác nhau, được chia thành các phần nhỏ để học sinh dễ dàng tiếp cận và giải quyết. Các câu hỏi thường yêu cầu học sinh:
Để giải câu a, ta cần xác định ma trận của phép biến hình affine. Dựa vào các thông tin cho trước, ta có thể thiết lập hệ phương trình để tìm các hệ số của ma trận. Sau khi tìm được ma trận, ta có thể áp dụng ma trận này để tìm ảnh của các điểm khác.
Ví dụ, nếu cho biết A(1; 2) biến thành A'(3; 4) qua phép biến hình affine f, ta có thể viết:
f(1; 2) = (3; 4)
Từ đó, ta có thể suy ra các hệ số của ma trận và giải hệ phương trình để tìm ra ma trận f.
Câu b thường yêu cầu tìm ảnh của một điểm hoặc một tập hợp điểm qua phép biến hình affine đã xác định ở câu a. Để làm điều này, ta chỉ cần nhân ma trận của phép biến hình affine với tọa độ của điểm cần tìm ảnh.
Ví dụ, nếu ta muốn tìm ảnh của điểm B(5; 6) qua phép biến hình affine f đã tìm được ở câu a, ta thực hiện phép nhân ma trận:
f(5; 6) = ma trận f * (5; 6)
Kết quả của phép nhân này sẽ là tọa độ của điểm B' là ảnh của điểm B qua phép biến hình affine f.
Câu c thường yêu cầu chứng minh một số tính chất liên quan đến phép biến hình affine. Để chứng minh, ta cần sử dụng các định nghĩa, tính chất của phép biến hình affine và các công cụ đại số để biến đổi các biểu thức toán học.
Ví dụ, ta có thể chứng minh rằng phép biến hình affine bảo toàn tính thẳng hàng của các điểm. Để chứng minh điều này, ta cần chứng minh rằng nếu ba điểm A, B, C thẳng hàng thì ba điểm A', B', C' cũng thẳng hàng.
Bài 6 trang 13 Sách bài tập Toán 11 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về phép biến hình affine. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập được cung cấp trong bài viết này, các bạn học sinh sẽ tự tin hơn khi giải quyết các bài toán liên quan đến phép biến hình affine.
| Công thức | Mô tả |
|---|---|
| Ma trận của phép biến hình affine | Cho phép biến hình affine f, ma trận của f có dạng: [[a, b, c], [d, e, f], [0, 0, 1]] |
| Phép biến hình affine | f(x; y) = (ax + by + c; dx + ey + f) |