Bài 2.23 trang 26 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.23 trang 26 sách bài tập Toán 10 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tổng các giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
Đề bài
Tổng các giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = x + 5y\) với \(\left( {x;y} \right)\) thuộc miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{ - 2 \le y \le 2}\\{x + y \le 4}\\{y - x \le 4}\end{array}} \right.\) là:
A. \( - 20.\)
B. \(-4.\)
C. \(28.\)
D. \( 16.\)
Phương pháp giải - Xem chi tiết
- Vẽ các bất phương trình trên cùng một mặt phẳng tọa độ \(Oxy.\)
- Xác định miền nghiệm của bất phương trình trên.
- Tìm tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức dựa vào miền nghiệm vừa xác định được.
Lời giải chi tiết
Miền nghiệm của bất phương trình \( - 2 \le y \le 2\) là miền nằm giữa hai đường thẳng \(d:y = - 2\) và \({d_1}:y = 2\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(x + y \le 4\) là nửa mặt phẳng bờ \({d_2}:x + y = 4\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(y - x \le 4\) là nửa mặt phẳng bờ \({d_3}:y - x = 4\) chứa gốc tọa độ \(O\left( {0;0} \right).\)
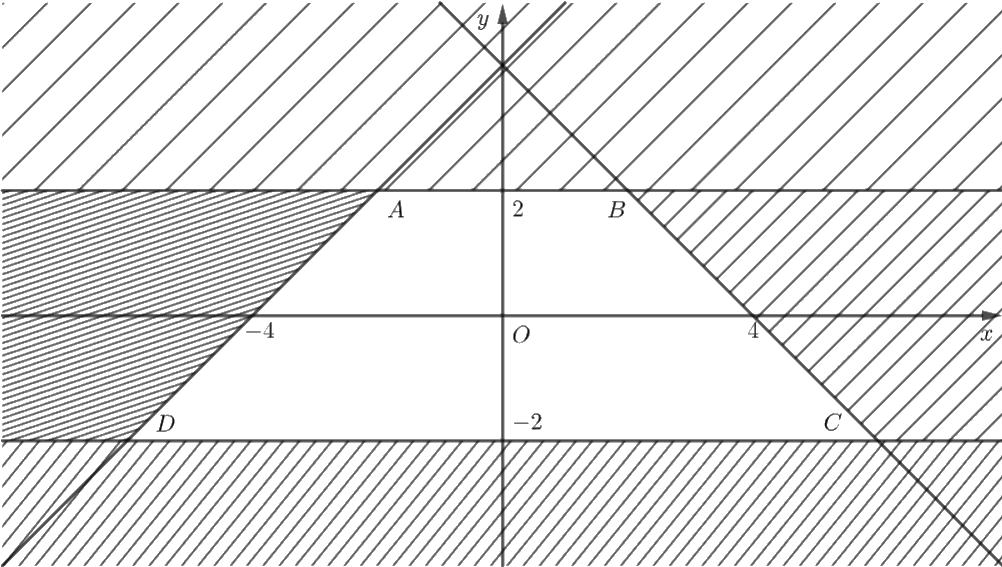
Miền nghiệm của hệ bất phương trình trên là hình thang cân \(ABCD\) với \(A\left( { - 2;2} \right),\) \(B\left( {2;2} \right),\) \(C\left( {6; - 2} \right),\) \(D\left( { - 6; - 2} \right).\)
Ta có: \(F\left( { - 2;2} \right) = - 2 + 5.2 = 8,\,\,F\left( {2;2} \right) = 2 + 5.2 = 12,\)
\(F\left( {6; - 2} \right) = 6 + 5\left( { - 2} \right) = - 4,\,\,F\left( { - 6; - 2} \right) = - 6 + 5\left( { - 2} \right) = - 16.\)
\( \Rightarrow \) giá trị lớn nhất của \(F\) là: \(F\left( {2;2} \right) = 12,\) giá trị nhỏ nhất của \(F\) là: \(F\left( { - 6; - 2} \right) = - 16.\)
Tổng giá trị lớn nhất và giá trị nhỏ nhất của \(F\) là: \(12 + \left( { - 16} \right) = - 4.\)
Chọn B.
Bài 2.23 trang 26 sách bài tập Toán 10 Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán liên quan đến vectơ, cụ thể là việc xác định mối quan hệ giữa các vectơ và tính toán độ dài của chúng. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Trước khi bắt tay vào giải bài toán, chúng ta cần đọc kỹ đề bài và xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Trong bài 2.23, chúng ta thường được cung cấp thông tin về các điểm trong mặt phẳng và yêu cầu xác định mối quan hệ giữa các vectơ được tạo bởi các điểm này. Ví dụ, chúng ta có thể được yêu cầu chứng minh rằng hai vectơ bằng nhau, song song, vuông góc hoặc tính độ dài của một vectơ.
Để giải bài 2.23 trang 26 sách bài tập Toán 10 Kết nối tri thức, chúng ta có thể áp dụng các bước sau:
Giả sử chúng ta có ba điểm A(1; 2), B(3; 4) và C(5; 6). Hãy tính vectơ AB và AC, sau đó xác định xem hai vectơ này có song song hay không.
Lời giải:
Vì vectơ AC = 2 * vectơ AB, nên hai vectơ AB và AC song song.
Khi giải các bài toán về vectơ, chúng ta cần chú ý đến các điều kiện của bài toán và lựa chọn phương pháp giải phù hợp. Ngoài ra, việc vẽ hình minh họa và kiểm tra lại kết quả là rất quan trọng để đảm bảo tính chính xác.
Để rèn luyện kỹ năng giải các bài toán về vectơ, bạn có thể tham khảo các bài tập tương tự trong sách bài tập Toán 10 Kết nối tri thức hoặc trên các trang web học toán online.
Bài 2.23 trang 26 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh nắm vững kiến thức về vectơ và các phép toán vectơ. Bằng cách áp dụng các bước giải chi tiết và lưu ý các điều kiện của bài toán, chúng ta có thể giải quyết bài toán này một cách hiệu quả.