Bài 6.12 trang 14 Sách bài tập Toán 10 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.12 trang 14 Sách bài tập Toán 10 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Hãy thực hiện các yêu cầu sau:
Đề bài
Với mỗi hàm số bậc hai cho dưới đây: \(y = f(x) = - {x^2} - x + 1\); \(y = g(x) = {x^2} - 8x + 8\)
Hãy thực hiện các yêu cầu sau:
a) Viết lại hàm số bậc hai dưới dạng \(y = a{(x - h)^2} + k\)
b) Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số
c) Vẽ đồ thị của hàm số
Lời giải chi tiết
a) Ta có:
\(y = f(x) = - {x^2} - x + 1 \Leftrightarrow f(x) = - \left( {{x^2} + x + \frac{1}{4}} \right) + \frac{5}{4} \Leftrightarrow f(x) = - {\left( {x + \frac{1}{2}} \right)^2} + \frac{5}{4}\)
\(y = g(x) = {x^2} - 8x + 8 \Leftrightarrow g(x) = {x^2} - 8x + 16 - 8 \Leftrightarrow g(x) = {(x - 4)^2} - 8\)
b) Ta có:
\(f(x) = - {\left( {x + \frac{1}{2}} \right)^2} + \frac{5}{4} \le \frac{5}{4}\) \( \Rightarrow \) GTLN của f(x) là \(\frac{5}{4}\) đạt được khi \(x = - \frac{1}{2}\)
\(g(x) = {(x - 4)^2} - 8 \ge - 8 \Rightarrow \) GTNN của g(x) là -8 đạt được khi x = 4
c)
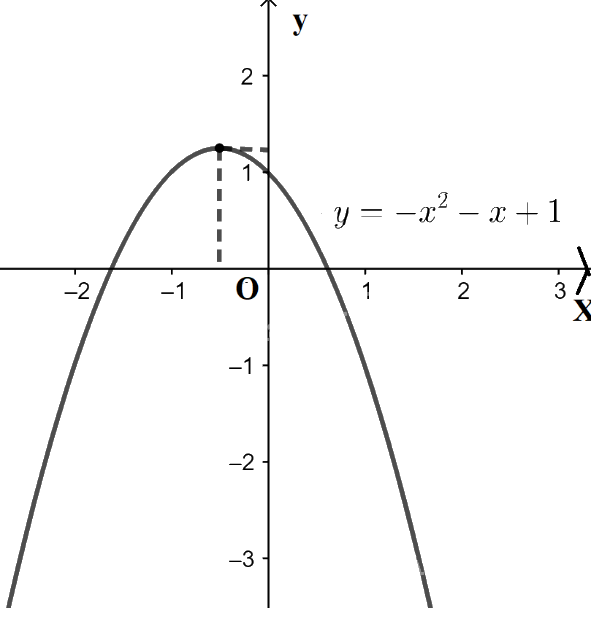
- Đồ thị hàm số \(y = - {x^2} - x + 1\) là đường parabol có a = -1 < 0 nên có bề lõm quay xuống dưới.
Đỉnh \(I\left( { - \frac{1}{2};\frac{5}{4}} \right)\), trục đối xứng x = \( - \frac{1}{2}\). Giao điểm của parabol với trục Oy là điểm (0 ; 1) và cắt trục Ox tại 2 điểm có hoành độ \(x = \frac{{ - 1 - \sqrt 5 }}{2}\) và \(x = \frac{{ - 1 + \sqrt 5 }}{2}\)
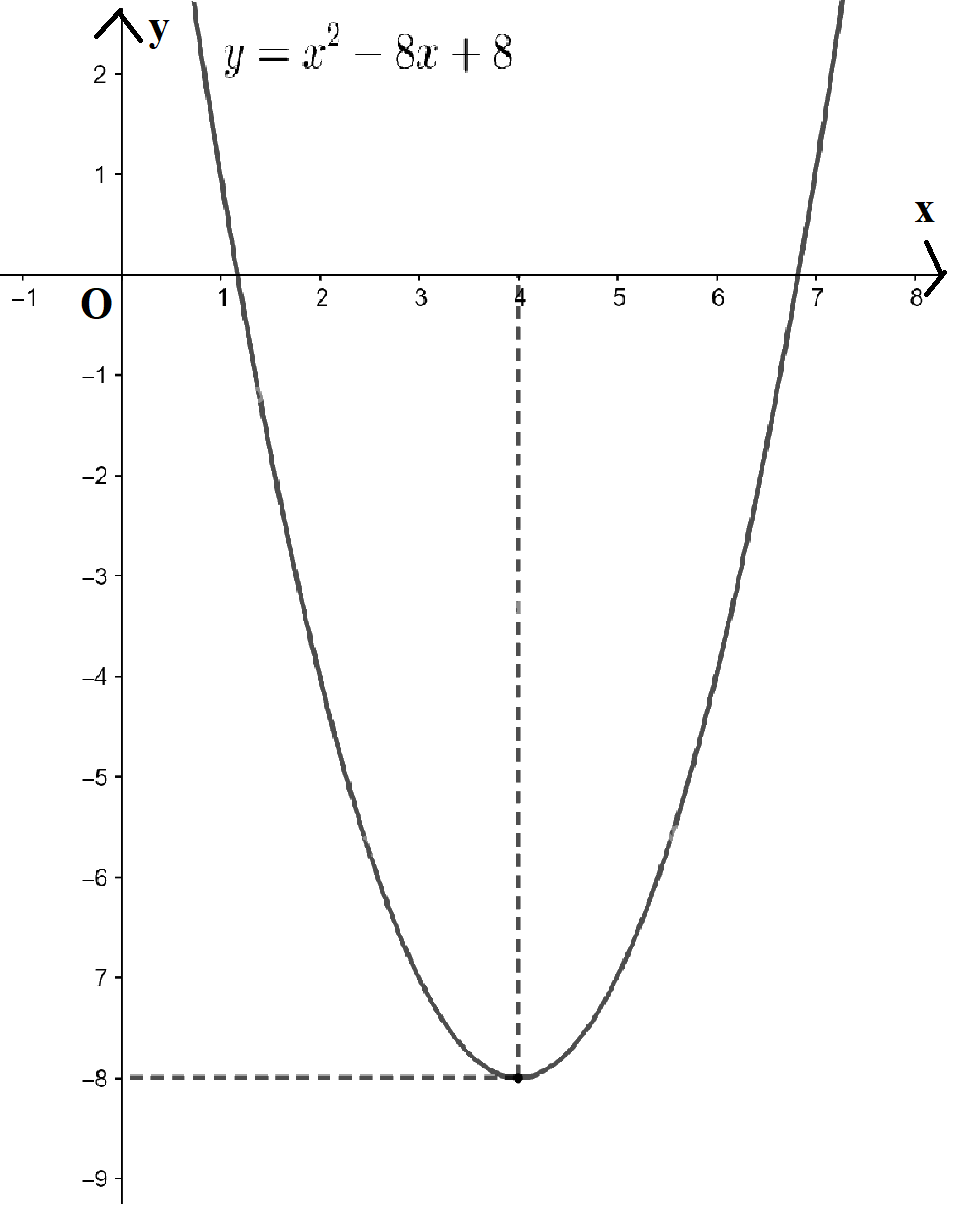
- Đồ thị hàm số \(y = {x^2} - 8x + 8\) là đường parabol có a = 1 > 0 nên có bề lõm quay lên trên
Đỉnh \(I(4; - 8)\), trục đối xứng x = 4. Giao điểm của parabol với trục Oy là điểm (0 ; 8) và cắt trục Ox tại 2 điểm có hoành độ \(x = 4 - 2\sqrt 2 \) và \(x = 4 + 2\sqrt 2 \)
Bài 6.12 trang 14 Sách bài tập Toán 10 - Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Nội dung bài tập 6.12: Bài tập thường yêu cầu học sinh chứng minh một đẳng thức vectơ, tìm tọa độ của một điểm hoặc vectơ, hoặc tính góc giữa hai vectơ. Để giải quyết bài tập này, học sinh cần phân tích đề bài, xác định các vectơ liên quan, và áp dụng các công thức và tính chất vectơ đã học.
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 6.12 trang 14, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài tập yêu cầu chứng minh đẳng thức vectơ AB + CD = AD + CB.
Ví dụ minh họa:
Cho bốn điểm A, B, C, D sao cho AB = DC. Chứng minh rằng AB + CD = AD + CB.
Giải:
Ta có: AB + CD = AB + BA + AC = AC + AC = 2AC
Và: AD + CB = AD + DB + BC = AB + BC = AC
Do đó, AB + CD ≠ AD + CB. (Lưu ý: Ví dụ này chỉ mang tính minh họa, cần kiểm tra lại điều kiện đề bài và áp dụng đúng quy tắc)
Lưu ý khi giải bài tập về vectơ:
Các bài tập tương tự:
Để rèn luyện kỹ năng giải bài tập về vectơ, các em có thể tham khảo các bài tập tương tự trong sách bài tập Toán 10 - Kết nối tri thức, hoặc tìm kiếm trên các trang web học toán online uy tín.
Kết luận:
Bài 6.12 trang 14 Sách bài tập Toán 10 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin giải quyết bài tập này một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!