Bài 2.29 trang 28 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bài tập này thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.29 trang 28, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Giả sử một người ăn kiêng cần được cung cấp ít nhất 300 calo, 36 đơn vị vitamin A và 90 đơn vị vitamin C mỗi ngày từ hai loại đồ uống / và //
Đề bài
Giả sử một người ăn kiêng cần được cung cấp ít nhất 300 calo, 36 đơn vị vitamin A và 90 đơn vị vitamin C mỗi ngày từ hai loại đồ uống / và //. Mỗi cốc đồ uống / cung cấp 60 calo, 12 đơn vị vitamin A và 10 đơn vị vitamin C.
Mỗi cốc đồ uống // cung cấp 60 calo, 6 đơn vị vitamin A và 30 đơn vị vitamin C. Biết rằng một cốc đồ uống / có giá 12 nghìn đồng và một cốc đồ uống // có giá 15 nghìn đồng.
a) Gọi x và y tương ứng là số cốc đồ uống / và //. Viết các phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình và xác định miền nghiệm của hệ đó.
b) Gọi F (nghìn đồng) là số tiền phải trả cho x cốc đồ uống / và y là số tiền phải trả cho y cốc đồ uống //. Hãy biểu diễn F theo x và y.
c) Biết rằng F đạt giá trị nhỏ nhất trên miền nghiệm tìm được ở câu a tại một trong các đỉnh của miền nghiệm, tìm giá trị nhỏ nhất đó. Từ đó suy ra người đó cần uống bao nhiêu cốc loại / và loại // để chi phí là nhỏ nhất. mà vẫn đáp ứng được yêu cầu hằng ngày.
Phương pháp giải - Xem chi tiết
- Viết các bất phương trình của bài toán trên.
- Xác định miền nghiệm của hệ bất phương trình đó.
- Viết biểu thức về số tiền phải trả cho 2 loại đồ uống.
- Tính giá trị nhỏ nhất về số tiền phải trả cho 2 loại đồ uống đo.
Lời giải chi tiết
a) Gọi x và y tương ứng là số cốc đồ uống / và //.
Điều kiện: \(x \ge 0;\,\,y \ge 0.\)
Số calo cần cung cấp cho người ăn kiêng từ hai loại đồ uống / và // là: \(60x + 60y \ge 300\,\, \Leftrightarrow \,\,x + y \ge 5.\)
Số vitamin A cần cung cấp cho người ăn kiêng từ hai loại đồ uống / và // là: \(12x + 6y \ge 36\,\, \Leftrightarrow \,\,2x + y \ge 6.\)
Số vitamin C cần cung cấp cho người ăn kiêng từ hai loại đồ uống / và // là: \(10x + 30y \ge 90\,\, \Leftrightarrow \,\,x + 3y \ge 9.\)
Ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{x + y \ge 5}\\{2x + y \ge 6}\\{x + 3y \ge 9}\end{array}.} \right.\)
Miền nghiệm của bất phương trình \(d:x \ge 0\) là nửa mặt phẳng bờ \(d\) chứa điểm \(\left( {1;0} \right).\)
Miền nghiệm của bất phương trình \({d_1}:y \ge 0\) là nửa mặt phẳng bờ \({d_1}\) chứa điểm \(\left( {0;1} \right).\)
Miền nghiệm của bất phương trình \(x + y \ge 5\) là nửa mặt phẳng bờ \({d_2}:x + y = 5\) không chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(2x + y \ge 6\) là nửa mặt phẳng bờ \({d_3}:2x + y = 6\) không chứa gốc tọa độ \(O\left( {0;0} \right).\)
Miền nghiệm của bất phương trình \(x + 3y \ge 9\) là nửa mặt phẳng bờ \({d_4}:x + 3y = 9\) không chứa gốc tọa độ \(O\left( {0;0} \right).\)
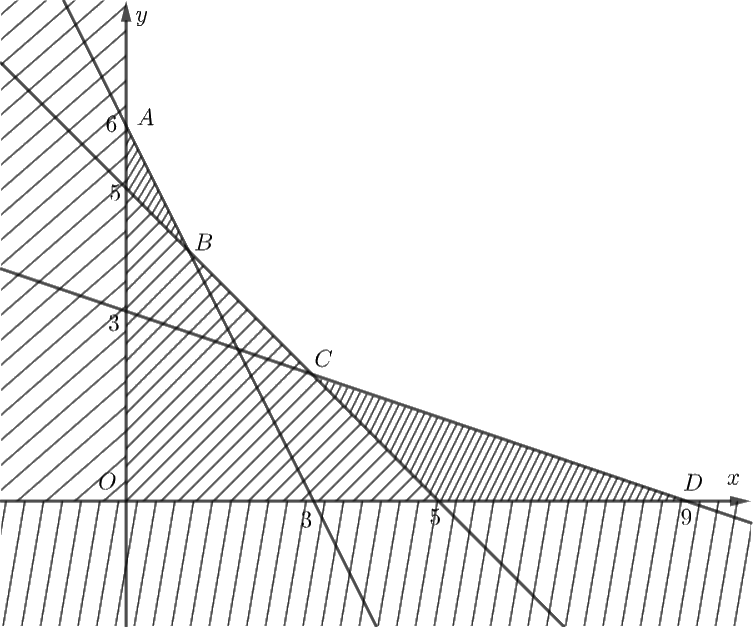
Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x \ge 0}\\{y \ge 0}\\{x + y \ge 5}\\{2x + y \ge 6}\\{x + 3y \ge 9}\end{array}} \right.\)là miền không bị gạch với \(A\left( {0;6} \right),\,\,B\left( {1;4} \right),\,\,C\left( {3;2} \right),\,\,D\left( {9;0} \right).\)
b) Số tiền phải trả cho hai loại đồ uống / và // là: \(F\left( {x;y} \right) = 12x + 15y\) (nghìn đồng).
c) Ta có: \(F\left( {0;6} \right) = 12.0 + 15.6 = 90,\,\,F\left( {1;4} \right) = 12.1 + 15.4 = 72,\)
\(F\left( {3;2} \right) = 12.3 + 15.2 = 66,\,\,F\left( {9;0} \right) = 12.9 + 15.0 = 108.\)
\( \Rightarrow \) Giá trị nhỏ nhất của \(F\) là \(F\left( {3;2} \right) = 66.\)
Vậy người đó cần uống 3 cốc đồ uống loại / và 2 cốc đồ uống loại // để đáp úng yêu cầu đặt ra hàng ngày.
Bài 2.29 trang 28 sách bài tập Toán 10 Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán liên quan đến vectơ, cụ thể là việc xác định mối quan hệ giữa các vectơ và sử dụng các phép toán vectơ để chứng minh một đẳng thức hoặc giải một bài toán hình học.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho tam giác ABC, gọi M là trung điểm của BC. Chứng minh rằng: 2MA + AB + AC = 0)
Để giải bài 2.29 trang 28, chúng ta cần nắm vững các kiến thức sau:
Bước 1: Phân tích bài toán
Đọc kỹ đề bài và xác định yêu cầu của bài toán. Trong bài toán này, chúng ta cần chứng minh một đẳng thức vectơ. Để chứng minh đẳng thức vectơ, chúng ta có thể sử dụng các phép biến đổi vectơ để đưa về một đẳng thức đúng.
Bước 2: Vẽ hình và đặt tên các vectơ
Vẽ hình minh họa bài toán và đặt tên các vectơ liên quan. Việc vẽ hình sẽ giúp chúng ta hình dung rõ hơn về bài toán và tìm ra phương pháp giải phù hợp.
Bước 3: Biến đổi vectơ
Sử dụng các quy tắc và tính chất của các phép toán vectơ để biến đổi biểu thức vectơ cho đến khi chứng minh được đẳng thức.
(Ví dụ lời giải cho đề bài giả định ở trên)
Ta có: MA = MB (vì M là trung điểm của BC)
=> 2MA = 2MB
=> 2MA + AB + AC = 2MB + AB + AC
Mà MB = MC => 2MB = BC
=> 2MA + AB + AC = BC + AB + AC
=> 2MA + AB + AC = (BC + AB) + AC
=> 2MA + AB + AC = AC + AC = 0 (do A, B, C thẳng hàng)
Để củng cố kiến thức về vectơ, bạn có thể làm thêm các bài tập tương tự trong sách bài tập Toán 10 Kết nối tri thức. Ngoài ra, bạn có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Giaitoan.edu.vn là một trang web học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán 10 Kết nối tri thức. Chúng tôi hy vọng rằng với sự hỗ trợ của Giaitoan.edu.vn, các em học sinh sẽ học Toán 10 một cách hiệu quả và đạt kết quả cao.
Hãy truy cập Giaitoan.edu.vn để khám phá thêm nhiều bài giải Toán 10 và các tài liệu học tập hữu ích khác!