Bài 7.18 trang 39 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.18 trang 39, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trong một hoạt động ngoại khóa của trường, lớp Việt định mở một gian hàng bán bánh mì và nước khoáng.
Đề bài
Trong một hoạt động ngoại khóa của trường, lớp Việt định mở một gian hàng bán bánh mì và nước khoáng. Biết rằng giá gốc một bánh mì là 15 000 đồng, một chai nước là 5 000 đồng. Các bạn dự kiến bán bánh mì với giá 20 000 đồng/ 1 bánh mì và nước giá 8 000 đồng/ 1 chai. Dựa vào thống kê số người tham gia hoạt động và nhu cầu thực tế các bạn dự kiến tổng số bánh mì và số chai nước không vượt quá 200. Theo quỹ lớp thì số tiền lớp Việt được dùng không quá 2 000 000 đồng. Hỏi lớp Việt có thể đạt được tối đa lợi nhuận là bao nhiêu?
Lời giải chi tiết
Gọi \(x,y\) lần lượt là số chiếc bánh mì và chai nước khoáng mà lớp Việt định mua để bán, Khi đó từ giả thiết ta có: \(x,y \in N\)
+ Ta có: \(\left\{ \begin{array}{l}x + y \le 200\\15000x + 5000y \le 2000000\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x + y \le 200\\3x + y \le 400\end{array} \right.\)
+ Nếu bán hết thì lợi nhuận lớp Việt có được là \(T = 5x + 3y\) (nghìn đồng)
+ Để tìm lợi nhuận lớn nhất ta cần tìm giá trị lớn nhất của biểu thức \(d:5x + 3y\)
+ Biểu diễn tập nghiệm của BPT: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 200\\3x + y \le 400\end{array} \right.\) trên mặt phẳng \(Oxy\), là miền tứ giác OABC
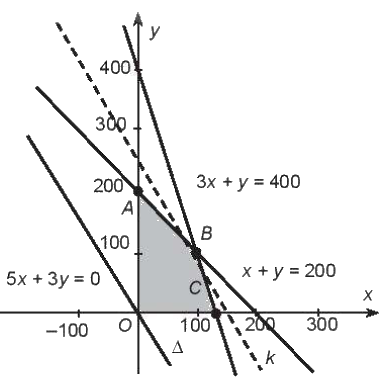
+ Khi đó các cặp \(\left( {x;y} \right)\) thỏa mãn đề bài là các cặp số tự nhiên sao cho điểm \(M\left( {x;y} \right)\) nằm trong miền tứ giác OABC
+ Ta có \(d = 5x + 3y = \sqrt {34} \frac{{\left| {5x + 3y} \right|}}{{\sqrt {{5^2} + {3^2}} }} = \sqrt {34} d\left( {M,\Delta } \right)\) với \(\Delta \) là đường thẳng có phương trình \(5x + 3y = 0\)
+ Gọi k là đường thẳng đi qua M và song song với \(\Delta \)/ Khi đó \(d\left( {M,\Delta } \right) = d\left( {k,\Delta } \right)\). Do đó d lớn nhất tương ứng với khoảng cách giữa k và \(\Delta \) lớn nhất.
+ Nhìn hình ta có khoảng cách giữa k và \(\Delta \) lớn nhất khi M trung B. Do đó giá tị lớn nhất của d là \(\sqrt {34} \frac{{\left| {5.100 + 3.100} \right|}}{{\sqrt {{5^2} + {3^2}} }} = 800\)
Vậy Lợi nhuận tối đa mà lớp Việt có thể đạt được là 800 nghìn đồng khi các bên mua và bán được 100 chiếc bánh mì và 100 chai nước
Bài 7.18 trang 39 sách bài tập Toán 10 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến vectơ và ứng dụng trong hình học. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Trước khi bắt tay vào giải bài toán, chúng ta cần đọc kỹ đề bài và xác định rõ các yếu tố sau:
Dưới đây là lời giải chi tiết bài 7.18 trang 39 sách bài tập Toán 10 Kết nối tri thức. (Nội dung lời giải chi tiết sẽ được trình bày tại đây, bao gồm các bước giải, giải thích rõ ràng và sử dụng các công thức toán học cần thiết. Ví dụ:)
Ví dụ lời giải (chỉ mang tính minh họa):
Cho tam giác ABC, với A(0;0), B(1;2), C(-1;0). Tìm tọa độ của vectơ AB và tính độ dài của vectơ AB.
Giải:
Vectơ AB có tọa độ là: AB = B - A = (1-0; 2-0) = (1; 2)
Độ dài của vectơ AB là: |AB| = √(12 + 22) = √5
Ngoài bài 7.18, sách bài tập Toán 10 Kết nối tri thức còn có nhiều bài tập tương tự về vectơ và ứng dụng trong hình học. Dưới đây là một số dạng bài tập thường gặp:
Để giải các bài tập về vectơ một cách hiệu quả, bạn có thể tham khảo một số mẹo sau:
Bài 7.18 trang 39 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
Hãy luyện tập thêm nhiều bài tập tương tự để nắm vững kiến thức và kỹ năng giải bài tập về vectơ nhé!