Bài 6.21 trang 18 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.21 trang 18, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Xét dấu các tam thức bậc hai sau:
Đề bài
Xét dấu các tam thức bậc hai sau:
a) \(f(x) = - {x^2} + 6x + 7\)
b) \(g(x) = 3{x^2} - 2x + 2\)
c) \(h(x) = - 16{x^2} + 24x - 9\)
d) \(k(x) = 2{x^2} - 6x + 1\)
Phương pháp giải - Xem chi tiết
Bước 1: Tính giá trị của ∆ (∆’), xét dấu hệ số a và ∆ (∆’)
Bước 2: Kết luận về dấu của tam thức bậc hai đã cho
Lời giải chi tiết
a) \(f(x) = - {x^2} + 6x + 7\) có ∆’ = 16 > 0, a = -1 < 0 và có 2 nghiệm phân biệt \({x_1} = - 1\); \({x_2} = 7\)
Do đó ta có bảng xét dấu f(x):
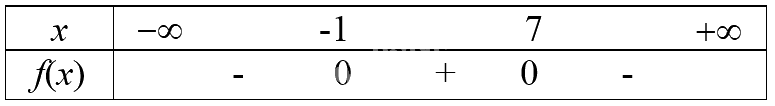
Suy ra \(f(x) > 0\)với mọi \(x \in ( - 1;7)\) và \(f(x) < 0\) với mọi \(x \in ( - \infty ; - 1) \cup (7; + \infty )\)
b) \(g(x) = 3{x^2} - 2x + 2\) có ∆’ = -5 < 0 và a = 3 > 0 nên g(x) > 0 với mọi \(x \in \mathbb{R}\)
c) \(h(x) = - 16{x^2} + 24x - 9\) có ∆’ = 0 và a = -16 < 0 nên h(x) có nghiệm kép \(x = \frac{3}{4}\) và \(h(x) < 0\) với mọi \(x \ne \frac{3}{4}\)
d) \(k(x) = 2{x^2} - 6x + 1\) có ∆’ = 7 > 0, a = 2 > 0 và có 2 nghiệm phân biệt \({x_1} = \frac{{3 - \sqrt 7 }}{2};{x_2} = \frac{{3 + \sqrt 7 }}{2}\)
Do đó ta có bảng xét dấu k(x):

Suy ra k(x) > 0 với mọi \(x \in \left( { - \infty ;\frac{{3 - \sqrt 7 }}{2}} \right) \cup \left( {\frac{{3 + \sqrt 7 }}{2}; + \infty } \right)\) và k(x) < 0 với mọi \(x \in \left( {\frac{{3 - \sqrt 7 }}{2};\frac{{3 + \sqrt 7 }}{2}} \right)\)
Bài 6.21 trang 18 sách bài tập Toán 10 Kết nối tri thức thường liên quan đến việc sử dụng các tính chất của vectơ, đặc biệt là các phép toán cộng, trừ vectơ, tích của một số với một vectơ, và các ứng dụng của vectơ trong việc chứng minh các tính chất hình học.
(Nội dung giải chi tiết bài 6.21 sẽ được trình bày ở đây. Ví dụ: Bài toán có thể yêu cầu chứng minh một đẳng thức vectơ, tìm tọa độ của một điểm, hoặc chứng minh một tính chất hình học. Lời giải sẽ bao gồm các bước thực hiện chi tiết, giải thích rõ ràng, và sử dụng các ký hiệu toán học chính xác.)
Ví dụ, giả sử bài toán yêu cầu chứng minh rằng tứ giác ABCD là hình bình hành, ta có thể sử dụng các tính chất sau:
Để chứng minh, ta cần biểu diễn các vectơ AB, DC, AD, BC theo các vectơ đơn vị hoặc các vectơ đã biết, sau đó sử dụng các tính chất và công thức để chứng minh đẳng thức hoặc tính song song.
Để củng cố kiến thức về vectơ và ứng dụng trong hình học, các em học sinh có thể tham khảo và giải các bài tập tương tự sau:
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết bài 6.21 trang 18 sách bài tập Toán 10 Kết nối tri thức sẽ giúp các em học sinh hiểu rõ hơn về vectơ và ứng dụng trong hình học, từ đó đạt kết quả tốt trong các kỳ thi.
| Công thức | Mô tả |
|---|---|
| a + b = b + a | Tính giao hoán của phép cộng vectơ |
| (a + b) + c = a + (b + c) | Tính kết hợp của phép cộng vectơ |
| k(a + b) = ka + kb | Tính chất phân phối của phép nhân số với vectơ đối với phép cộng vectơ |