Bài 3.28 trang 41 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng của vectơ trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.28 trang 41, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Diện tích của tam giác bằng:
Đề bài
Cho tam giác \(ABC\) có \(a = 20,\,\,b = 16\) và \({m_a} = 10.\) Diện tích của tam giác bằng:
A. \(92.\)
B. \(100.\)
C. \(96.\)
D. \(88.\)
Phương pháp giải - Xem chi tiết
- Tính nửa chu vi \(\Delta AMC\): \(p = \frac{{\frac{a}{2} + {m_a} + b}}{2}\)
- Tính diện tích \(\Delta AMC\): \({S_{\Delta AMC}} = \sqrt {p\left( {p - \frac{a}{2}} \right)\left( {p - {m_a}} \right)\left( {p - b} \right)} \)
- Diện tích \(\Delta ABC\): \(S = 2{S_{\Delta AMC}}\)
Lời giải chi tiết
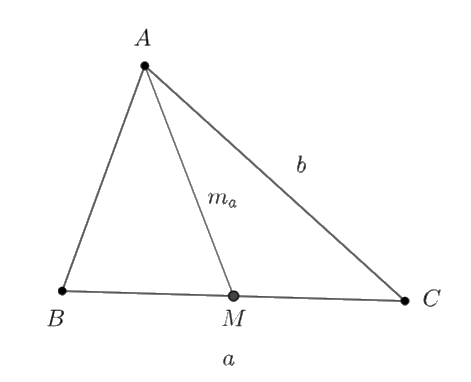
Nửa chu vi \(\Delta AMC\) là: \(p = \frac{{\frac{a}{2} + {m_a} + b}}{2} = \frac{{10 + 10 + 16}}{2} = 18.\)
Diện tích \(\Delta AMC\) là:
\({S_{\Delta AMC}} = \sqrt {p\left( {p - \frac{a}{2}} \right)\left( {p - {m_a}} \right)\left( {p - b} \right)} = \sqrt {18\left( {18 - 10} \right)\left( {18 - 10} \right)\left( {18 - 16} \right)} = 48.\)
Diện tích \(\Delta ABC\) là: \(S = 2{S_{\Delta AMC}} = 2.48 = 96\)
Chọn C.
Bài 3.28 trang 41 sách bài tập Toán 10 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến vectơ, thường là xác định mối quan hệ giữa các vectơ hoặc tính toán các đại lượng hình học sử dụng vectơ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Phân tích bài toán:
Trước khi bắt tay vào giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Vẽ hình minh họa (nếu cần thiết) để hình dung rõ hơn về bài toán. Xác định các vectơ liên quan và mối quan hệ giữa chúng.
Lời giải chi tiết:
Để cung cấp một lời giải chi tiết, chúng ta cần biết chính xác nội dung của bài 3.28 trang 41. Tuy nhiên, dựa trên kinh nghiệm giải các bài tập tương tự, chúng ta có thể đưa ra một số hướng giải quyết phổ biến:
Ví dụ minh họa (giả định bài toán):
Giả sử bài 3.28 yêu cầu chứng minh rằng tứ giác ABCD là hình bình hành. Chúng ta có thể giải bài toán như sau:
Lời giải:
Gọi A, B, C, D là các đỉnh của tứ giác. Ta cần chứng minh rằng AB = CD và AB song song CD (hoặc AD = BC và AD song song BC).
Sử dụng vectơ, ta có:
AB = B - A
CD = D - C
Để chứng minh AB = CD, ta cần chứng minh AB = CD (tức là hai vectơ bằng nhau).
Để chứng minh AB song song CD, ta cần chứng minh AB = k.CD (với k là một số thực khác 0).
Lưu ý:
Trong quá trình giải bài tập, học sinh cần chú ý đến việc sử dụng đúng các ký hiệu vectơ và các phép toán trên vectơ. Kiểm tra lại kết quả để đảm bảo tính chính xác. Nếu gặp khó khăn, hãy tham khảo các tài liệu tham khảo hoặc hỏi ý kiến giáo viên, bạn bè.
Mở rộng:
Các bài tập về vectơ có nhiều ứng dụng trong thực tế, chẳng hạn như trong việc xác định vị trí, hướng đi của các vật thể, trong việc giải các bài toán vật lý, kỹ thuật. Việc nắm vững kiến thức về vectơ sẽ giúp học sinh giải quyết các bài toán thực tế một cách hiệu quả.
Tổng kết:
Bài 3.28 trang 41 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ. Bằng cách nắm vững các kiến thức cơ bản và áp dụng các phương pháp giải phù hợp, học sinh có thể tự tin giải quyết bài tập này và các bài tập tương tự.