Bài 1.39 trang 15 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về vectơ vào giải quyết các bài toán hình học. Bài tập này thường yêu cầu học sinh xác định các vectơ, tính toán độ dài vectơ, và chứng minh các đẳng thức vectơ.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.39 trang 15, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Hãy điền Đ vào ô trống nếu mệnh đề đúng, điền S vào ô trống nếu mệnh đề sai.
Đề bài
Cho các tập hợp sau:
A ={x là số nguyên tố và \(20 \le x \le 30\)}
B ={x là bội của 18 và \(20 \le x \le 30\)}
C là tập hợp các nghiệm dương của phương trình \({x^3} - 52{x^2} + 667x = 0.\)
Hãy điền Đ vào ô trống nếu mệnh đề đúng, điền S vào ô trống nếu mệnh đề sai.
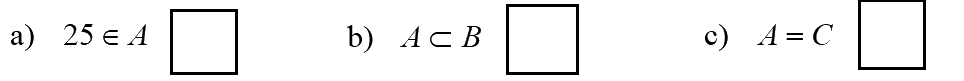
Phương pháp giải - Xem chi tiết
- Giải phương trình \({x^3} - 52{x^2} + 667x = 0.\)
- Liệt kê các phần tử thỏa mãn các tập hợp đã cho.
- Điền Đ hoặc S vào ô trống.
Lời giải chi tiết
Giải phương trình \({x^3} - 52{x^2} + 667x = 0\,\, \Leftrightarrow \,\,\left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 23}\\{x = 29}\end{array}.} \right.\)
Vì phương trình lấy nghiệm dương nên \(x = 23\) và \(x = 29\) thỏa mãn.
\(A = \left\{ {23;29} \right\};\quad B = \emptyset ;\quad C = \left\{ {23;29} \right\}.\)
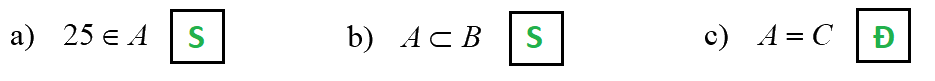
Bài 1.39 trang 15 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết một bài toán cụ thể. Để giải bài này, chúng ta cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, bài toán sẽ cung cấp một hình vẽ hoặc một mô tả về các điểm và vectơ liên quan. Chúng ta cần vẽ lại hình vẽ (nếu cần) và đánh dấu các yếu tố quan trọng để dễ dàng theo dõi.
Dưới đây là lời giải chi tiết bài 1.39 trang 15 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống. (Nội dung lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, các công thức sử dụng, và các giải thích rõ ràng. Ví dụ:)
Ví dụ lời giải:
Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng vectơ AM = (1/2)vectơ(AB) + vectơ(AD).
Vì M là trung điểm của BC, ta có vectơ BM = (1/2)vectơ BC. Mà vectơ BC = vectơ AD (do ABCD là hình bình hành). Do đó, vectơ BM = (1/2)vectơ AD.
Áp dụng quy tắc cộng vectơ, ta có vectơ AM = vectơ AB + vectơ BM = vectơ AB + (1/2)vectơ AD.
Vậy, vectơ AM = (1/2)vectơ(AB) + vectơ(AD).
Ngoài bài 1.39, sách bài tập Toán 10 - Kết nối tri thức với cuộc sống còn có nhiều bài tập tương tự về vectơ. Các bài tập này thường yêu cầu học sinh:
Để giải tốt các bài tập về vectơ, bạn có thể tham khảo một số mẹo sau:
Bài 1.39 trang 15 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải toán. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn khi làm bài tập về vectơ.
Hãy tiếp tục luyện tập và khám phá thêm nhiều bài tập thú vị khác trên Giaitoan.edu.vn để nâng cao kiến thức Toán 10 của bạn!