Bài 4.17 trang 54 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.17 trang 54, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho lục giác ABCDEF. Gọi M,N,P,Q,R,S theo thứ tự là trung điểm của các cạnh AB,BC,CD,DE,EF,FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Đề bài
Cho lục giác \(ABCDEF.\) Gọi \(M,\,\,N,\,\,P,\,\,Q,\,\,R,\,\,S\) theo thứ tự là trung điểm của các cạnh \(AB,\;\,BC,\,\,CD,\,\,DE,\,\,EF,\,\,FA.\) Chứng minh rằng hai tam giác \(MPR\) và \(NQS\) có cùng trọng tâm.
Lời giải chi tiết
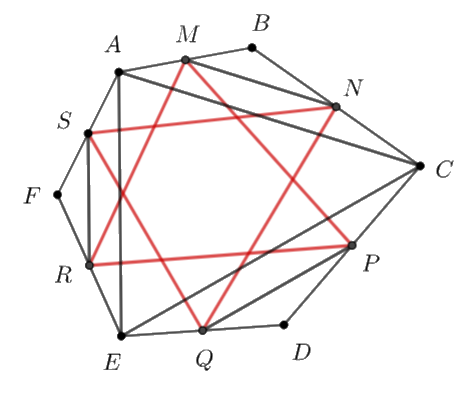
Ta có: \(MN\)là đường trung bình của \(\Delta ABC\)
\( \Rightarrow \) \(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {AC} \) (1)
Chứng minh tương tự ta được: \(\overrightarrow {PQ} = \frac{1}{2}\overrightarrow {CE} \) và \(\overrightarrow {RS} = \frac{1}{2}\overrightarrow {EA} \) (2)
Từ (1) và (2) \( \Rightarrow \) \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {EA} } \right) = \frac{1}{2}\left( {\overrightarrow {AE} + \overrightarrow {EA} } \right) = \overrightarrow 0 \)
\( \Rightarrow \) hai tam giác \(MPR\) và \(NQS\) có cùng trọng tâm.
Bài 4.17 trang 54 sách bài tập Toán 10 Kết nối tri thức yêu cầu học sinh sử dụng kiến thức về vectơ để chứng minh một số tính chất hình học. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Trước khi bắt tay vào giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Thông thường, bài toán sẽ yêu cầu chúng ta chứng minh một đẳng thức vectơ hoặc một tính chất hình học nào đó. Sau đó, chúng ta cần tìm ra phương pháp giải phù hợp. Một số phương pháp thường được sử dụng để giải các bài toán về vectơ bao gồm:
(Giả sử đề bài là: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2 )
Lời giải:
Vì M là trung điểm của BC, ta có: overrightarrow{BM} =overrightarrow{MC}.
Ta có: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{BM}.
Mà overrightarrow{BM} = (1/2)overrightarrow{BC} = (1/2)(overrightarrow{AC} -overrightarrow{AB}).
Do đó: overrightarrow{AM} =overrightarrow{AB} + (1/2)(overrightarrow{AC} -overrightarrow{AB}) =overrightarrow{AB} + (1/2)overrightarrow{AC} - (1/2)overrightarrow{AB} = (1/2)overrightarrow{AB} + (1/2)overrightarrow{AC} = (overrightarrow{AB} +overrightarrow{AC})/2.
Khi giải các bài tập về vectơ, chúng ta cần lưu ý một số điều sau:
Để củng cố kiến thức về vectơ, các em có thể làm thêm một số bài tập tương tự sau:
Bài 4.17 trang 54 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin giải bài tập này và các bài tập tương tự.