Bài 4.12 trang 51 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.12 trang 51, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trên mặt phẳng, chất điểm A chịu tác động của ba lực
Đề bài
Trên mặt phẳng, chất điểm \(A\) chịu tác động của ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) và ở trạng thái cân bằng. Góc giữa hai vectơ \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} \) bằng \({60^ \circ }.\) Tính độ lớn của \(\overrightarrow {{F_3}} ,\) biết rằng \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = 2\sqrt 3 N.\)
Phương pháp giải - Xem chi tiết
- Chứng minh tứ giác \(ABEC\) là hình thoi
- Tính cạnh \(AE\): \(AE = 2.\frac{{AB\sqrt 3 }}{2} = AB\sqrt 3 \)
- Do vật ở vị trí cân bằng nên \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow F } \right| = AE\)
Lời giải chi tiết
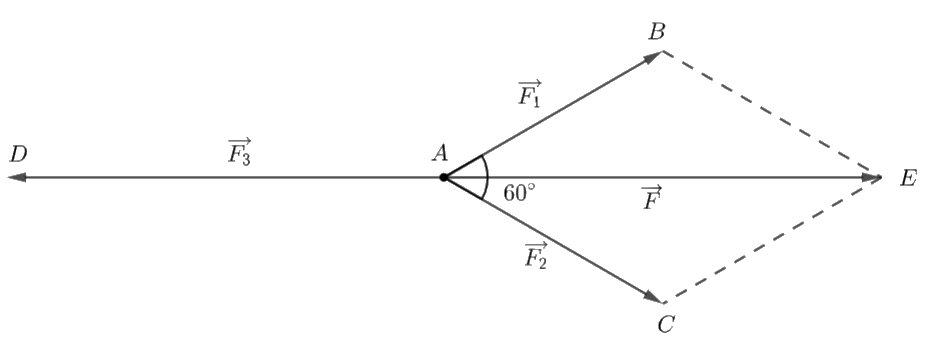
Giả sử \(\overrightarrow {AB} ,\,\,\overrightarrow {AC} ,\,\,\overrightarrow {AD} \) lần lượt biểu thị cho các lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) và vectơ \(\overrightarrow {AE} \) biểu thị cho hợp lực của hai lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} \)
Ta có: tứ giác \(ABEC\) là hình bình hành
mặt khắc \(\widehat {BAC} = {60^ \circ }\)
nên tứ giác \(ABEC\) là hình thoi
\( \Rightarrow \) \(\Delta ABC\) là tam giác đều
\( \Rightarrow \) \(AE = 2.\frac{{2\sqrt 3 .\sqrt 3 }}{2} = 6\,\,(N)\)
Do vật ở vị trí cân bằng nên hai lực \(\overrightarrow F \) và \(\overrightarrow {{F_3}} \) có cùng cường độ và ngược chiều nhau
\( \Rightarrow \) \(\left| {\overrightarrow {F{}_3} } \right| = \left| {\overrightarrow F } \right| = AE = 6\,\,(N)\)
Bài 4.12 trang 51 sách bài tập Toán 10 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến vectơ, thường là xác định mối quan hệ giữa các vectơ hoặc tính toán các đại lượng hình học sử dụng vectơ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Trước khi bắt tay vào giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, cần phân tích bài toán để tìm ra mối liên hệ giữa các yếu tố đã cho và yêu cầu của bài toán. Việc vẽ hình minh họa có thể giúp học sinh hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
(Giả sử bài toán cụ thể là: Cho tam giác ABC. Gọi M là trung điểm của BC. Tìm vectơ AM theo vectơ AB và AC.)
Lời giải:
Ta có: AM = AB + BM
Vì M là trung điểm của BC nên BM = MC = 1/2 BC
Mà BC = AC - AB
Do đó, BM = 1/2 (AC - AB)
Thay vào phương trình ban đầu, ta được:
AM = AB + 1/2 (AC - AB) = 1/2 AB + 1/2 AC
Vậy AM = 1/2 (AB + AC)
Ngoài bài 4.12, sách bài tập Toán 10 Kết nối tri thức còn nhiều bài tập tương tự về vectơ. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức cơ bản về vectơ và các phép toán trên vectơ. Ngoài ra, cần rèn luyện kỹ năng phân tích bài toán và tìm ra hướng giải quyết phù hợp.
Để củng cố kiến thức về vectơ và rèn luyện kỹ năng giải bài tập, học sinh có thể tham khảo thêm các bài tập sau:
Bài 4.12 trang 51 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên đây, các em học sinh sẽ hiểu rõ hơn về bài tập này và tự tin làm bài tập.