Bài 6.42 trang 24 Sách bài tập Toán 10 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.42 trang 24 Sách bài tập Toán 10 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Đường Parabol trong hình dưới đây là đồ thị của hàm số nào?
Đề bài
Đường Parabol trong hình dưới đây là đồ thị của hàm số nào?
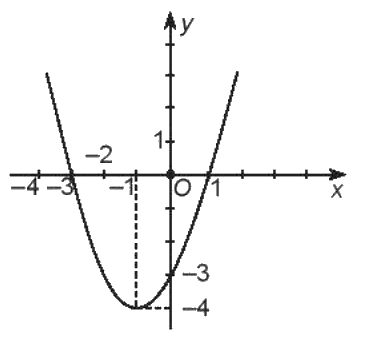
A. \(y = {x^2} + 2x - 3\)
B. \(y = - {x^2} - 2x + 3\)
C. \(y = - {x^2} + 2x - 3\)
D. \(y = {x^2} - 2x - 3\)
Lời giải chi tiết
Đường Parabol có bề lõm quay lên trên nên a > 0 => Loại B, C
Ta có: \( - \frac{b}{{2a}} = - 1 < 0\) mà a > 0 nên b > 0 => Loại D
\( \Rightarrow \) Chọn A
Bài 6.42 trang 24 Sách bài tập Toán 10 - Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Dưới đây là đề bài và lời giải chi tiết bài 6.42 trang 24 Sách bài tập Toán 10 - Kết nối tri thức:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SB và mặt phẳng (ABCD).
Bước 1: Xác định các yếu tố cần thiết
Để tính góc giữa đường thẳng SB và mặt phẳng (ABCD), ta cần tìm hình chiếu của SB lên mặt phẳng (ABCD). Gọi H là hình chiếu của S lên mặt phẳng (ABCD). Do SA vuông góc với (ABCD) nên H trùng với A.
Bước 2: Tính độ dài các cạnh
Ta có: AB = a, SA = a. Trong tam giác vuông SAB, ta có:
SB = √(SA2 + AB2) = √(a2 + a2) = a√2
Bước 3: Tính góc giữa SB và mặt phẳng (ABCD)
Gọi φ là góc giữa đường thẳng SB và mặt phẳng (ABCD). Ta có:
sin φ = SA / SB = a / (a√2) = 1/√2 = √2 / 2
Suy ra: φ = 45o
Kết luận: Góc giữa đường thẳng SB và mặt phẳng (ABCD) là 45o.
Ngoài bài 6.42, còn rất nhiều bài tập tương tự liên quan đến góc giữa đường thẳng và mặt phẳng. Để giải các bài tập này, học sinh cần:
Một số dạng bài tập thường gặp:
Để củng cố kiến thức và kỹ năng giải bài tập về góc giữa đường thẳng và mặt phẳng, các em học sinh nên luyện tập thêm các bài tập sau:
Bài 6.42 trang 24 Sách bài tập Toán 10 - Kết nối tri thức là một bài tập điển hình về ứng dụng của vectơ trong không gian. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp các em học sinh tự tin hơn trong quá trình học tập môn Toán 10.
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ hiểu rõ hơn về bài tập này và có thể tự giải các bài tập tương tự một cách dễ dàng.