Bài 4.31 trang 65 sách bài tập Toán 10 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.31 trang 65, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
a) AM vuông góc với DE. b) BE vuông góc với CD. c) Tam giác MNP là một tam giác vuông cân
Đề bài
Cho tam giác \(ABC\) có \(\widehat A < {90^ \circ }.\) Dựng ra phía ngoài tam giác hai tam giác vuông cân đỉnh \(A\) là \(ABD\) và \(ACE.\) Gọi \(M,\,\,N,\,\,P\) theo thứ tự là trung điểm \(BC,\,\,BD,\,\,CE.\) Chứng minh rằng:
a) \(AM\) vuông góc với \(DE.\)
b) \(BE\) vuông góc với \(CD.\)
c) Tam giác \(MNP\) là một tam giác vuông cân.
Phương pháp giải - Xem chi tiết
- Tính các vectơ \(\overrightarrow {AM} \) và \(\overrightarrow {DE} \) xong chứng minh tích vô hướng \(\overrightarrow {AM} .\overrightarrow {DE} = 0\)
- Tính các vectơ \(\overrightarrow {BE} \) và \(\overrightarrow {CD} \) xong chứng minh tích vô hướng \(\overrightarrow {BE} .\overrightarrow {CD} = 0\)
- Chứng minh \(MN\)//\(CD\) và \(MP\)//\(BE\)
Lời giải chi tiết
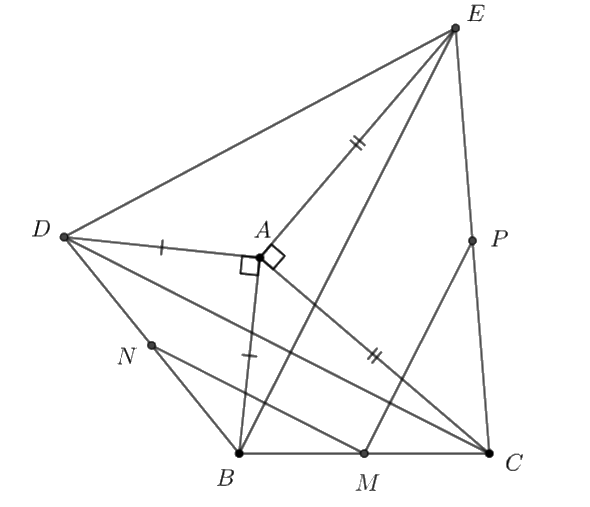
a) Ta có: \(\overrightarrow {DE} = \overrightarrow {AE} - \overrightarrow {AD} \) và \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
\( \Rightarrow \overrightarrow {AM} .\overrightarrow {DE} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\left( {\overrightarrow {AE} - \overrightarrow {AD} } \right)\)
\(\begin{array}{l} = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AE} - \overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AC} .\overrightarrow {AE} - \overrightarrow {AC} .\overrightarrow {AD} } \right)\\ = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AE} - \overrightarrow {AC} .\overrightarrow {AD} } \right)\\ = \frac{1}{2}\left( {AB.AE.\cos \widehat {BAE} - AC.AD.\cos \widehat {CAD}} \right) = 0\end{array}\)
\( \Rightarrow \) \(\overrightarrow {AM} \bot \overrightarrow {DE} \) \( \Rightarrow \) \(AM \bot DE\)
b) Ta có: \(\overrightarrow {BE} = \overrightarrow {AE} - \overrightarrow {AB} \) và \(\overrightarrow {CD} = \overrightarrow {AD} - \overrightarrow {AC} \)
\( \Rightarrow \) \(\overrightarrow {BE} .\overrightarrow {CD} = \left( {\overrightarrow {AE} - \overrightarrow {AB} } \right)\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right)\)
\(\begin{array}{l} = \overrightarrow {AE} .\overrightarrow {AD} - \overrightarrow {AE} .\overrightarrow {AC} - \overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} .\overrightarrow {AC} \\ = \overrightarrow {AE} .\overrightarrow {AD} + \overrightarrow {AB} .\overrightarrow {AC} \\ = AE.AD.\cos \widehat {DAE} + AB.AC.\cos \widehat {BAC}\\ = AE.AD.\cos \widehat {DAE} + AB.AC.\cos \left( {{{180}^ \circ } - \widehat {DAE}} \right) = 0\end{array}\)
\( \Rightarrow \) \(\overrightarrow {BE} \bot \overrightarrow {CD} \) \( \Rightarrow \) \(BE \bot CD\)
c) Ta có: \(MN\) và \(MP\) lần lượt là đường trung bình của \(\Delta BCD\) và \(\Delta ACE\)
\( \Rightarrow \) \(MN\)//\(CD\) và \(MP\)//\(BE\)
mặt khác \(CD \bot BE\) (cm câu b)
\( \Rightarrow \) \(MN \bot MP\)
\( \Rightarrow \) \(\Delta MNP\) vuông tại \(M\)
+
Xét \(\Delta ADC\) và \(\Delta ABE\) ta có:
\(AD = AB\)
\(AC = AE\)
\(\widehat {DAC} = \widehat {BAE} = {90^o} + \widehat {BAC}\)
\( \Rightarrow \Delta ADC = \Delta ABE\) (cạnh góc cạnh)
\( \Rightarrow DC = BE\)
Lại có: \(MN = \frac{1}{2}DC\) (do M, N là trung điểm BD, BC)
\(MP = \frac{1}{2}BE\) (do M, N là trung điểm CB, CE)
\( \Rightarrow MN = MP\)
Vậy tam giác MNP vuông cân tại M.
Bài 4.31 trang 65 sách bài tập Toán 10 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến vectơ và ứng dụng trong hình học. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Nội dung bài toán: (Giả sử bài toán cụ thể là: Cho tam giác ABC, tìm tập hợp các điểm M sao cho MA + MB = MC)
Để giải bài toán này, chúng ta sẽ sử dụng các kiến thức về vectơ và phép cộng, trừ vectơ. Cụ thể:
Ví dụ minh họa:
Giả sử A(0;0), B(a;0), C(b;c). Khi đó:
Phương trình MA + MB = MC trở thành:
(x; y) + (x - a; y) = (x - b; y - c)
Giải phương trình này, ta sẽ tìm được tọa độ của điểm M thỏa mãn điều kiện bài toán.
Mở rộng kiến thức:
Ngoài bài 4.31, các em học sinh có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 10 Kết nối tri thức để rèn luyện kỹ năng giải toán về vectơ. Bên cạnh đó, các em cũng có thể tìm hiểu thêm về các ứng dụng của vectơ trong các lĩnh vực khác như vật lý, kỹ thuật.
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về bài 4.31 trang 65 sách bài tập Toán 10 Kết nối tri thức và tự tin làm bài tập. Chúc các em học tập tốt!