Bài 2.6 trang 23 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, phép toán vectơ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.6 trang 23, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Biểu diễn miền nghiệm của các hệ bất phương trình sau trên mặt phẳng tọa độ:
Đề bài
Biểu diễn miền nghiệm của các hệ bất phương trình sau trên mặt phẳng tọa độ:
a) \(\left\{ {\begin{array}{*{20}{c}}{x \ge - 1}\\{y \ge 0}\\{x + y \le 4}\end{array}} \right.\)
b) \(\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{y > 0}\\{x - y - 4 < 0}\end{array}} \right.\)
c) \(\left\{ {\begin{array}{*{20}{c}}{y \le 3}\\{x \le 3}\\{x \ge - 1}\\{y \ge - 2}\end{array}} \right.\)
Phương pháp giải - Xem chi tiết
- Vẽ các hệ bất phương trình trên mặt phẳng tọa độ \(Oxy.\)
- Nhìn vào đồ thị xác định miền nghiệm của hệ bất phương trình đã cho.
Lời giải chi tiết
a) \(\left\{ {\begin{array}{*{20}{c}}{x \ge - 1}\\{y \ge 0}\\{x + y \le 4}\end{array}} \right.\)
Xác định miền nghiệm của bất phương trình \(x \ge - 1\) là nửa mặt phẳng bờ \(d:x = - 1\) chứa điểm \(O\left( {0;0} \right).\)
Xác định miền nghiệm của bất phương trình \(y \ge 0\) là nửa mặt phẳng bờ \(Ox\) chứa điểm \(\left( {0;4} \right).\)
Xác định miền nghiệm của bất phương trình\(x + y \le 4.\)
Vẽ đường thẳng \({d_2}:x + y = 4\) trên mặt phẳng tọa độ \(Oxy.\)
Chọn \(O\left( {0;0} \right)\) là điểm không thuộc đường thẳng \({d_2}\) và thay vào biểu thức \(x + y,\) ta được \(0 + 0 = 0 < 4.\)
Do đó, miền nghiệm của bất phương trình \({d_2}:x + y = 4\) là nửa mặt phẳng bờ \({d_2}\) và chứa điểm \(O\left( {0;0} \right).\)
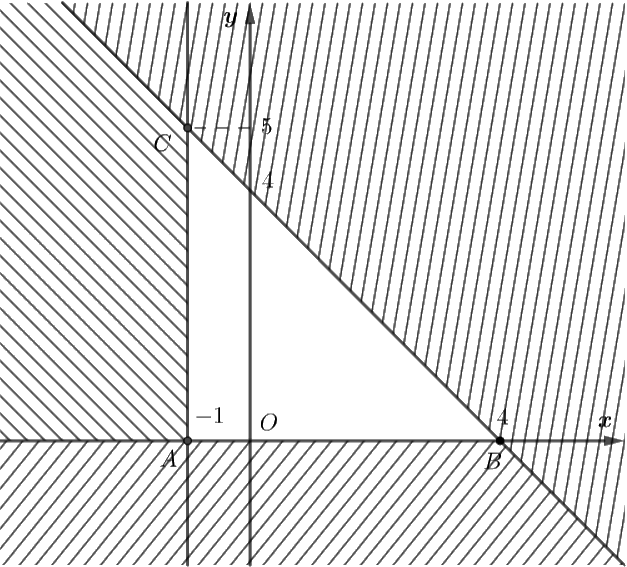
Vậy miền nghiệm của hệ bất phương trình trên là: \(\Delta ABC\) với \(A\left( { - 1;0} \right),\,\,B\left( {4;0} \right),\,\,C\left( { - 1;5} \right).\)
b) \(\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{y > 0}\\{x - y - 4 < 0}\end{array}} \right.\)
Xác định miền nghiệm của bất phương trình \(x > 0\) là nửa mặt phẳng bờ \(Oy\) chứa điểm \(\left( {1;0} \right)\) mà bỏ đi trục \(Oy.\)
Xác định miền nghiệm của bất phương trình \(y > 0\) là nửa mặt phẳng bờ \(Ox\) chứa điểm \(\left( {0;1} \right)\) mà bỏ đi trục \(Ox.\)
Xác định miền nghiệm của bất phương trình \(x - y - 4 < 0\).
Vẽ đường thẳng \({d_2}:x - y - 4 = 0\) trên mặt phẳng tọa độ \(Oxy.\)
Chọn \(O\left( {0;0} \right)\) không thuộc đường thẳng \({d_2}\) và thay vào biểu thức \(x - y - 4,\) ta được \(0 - 0 - 4 = - 4 < 0.\)
Do đó, miền nghiệm của bất phương trình \(x - y - 4 < 0\) là nửa mặt phẳng bờ \({d_2}\) chứa điểm \(O\left( {0;0} \right)\) không kể \({d_2}\).
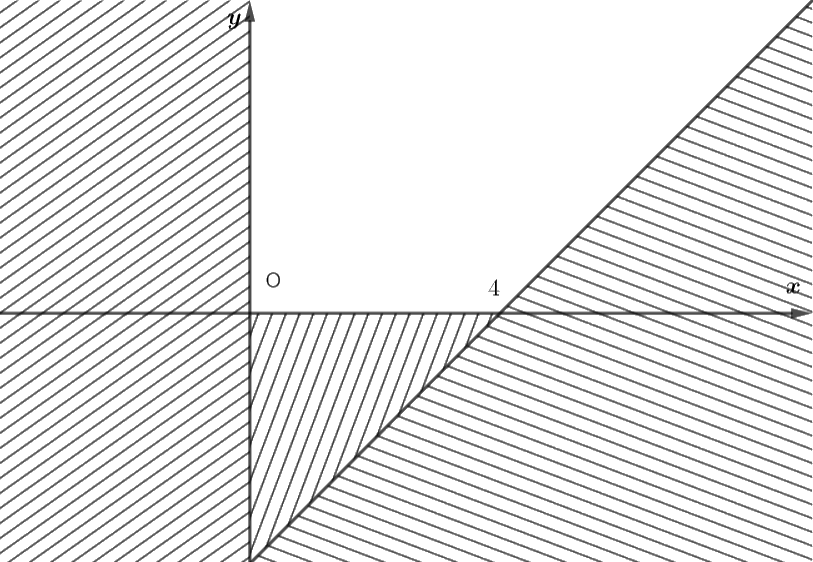
Miền nghiệm của hệ bất phương trình trên là phần không có gạch.
c) \(\left\{ {\begin{array}{*{20}{c}}{y \le 3}\\{x \le 3}\\{x \ge - 1}\\{y \ge - 2}\end{array}} \right.\)
Xác định miền nghiệm của bất phương trình \(y \le 3\) là nửa mặt phẳng bờ \(d:y = 3\) chứa điểm \(O\left( {0;0} \right).\)
Xác định miền nghiệm của bất phương trình \(x \le 3\) là nửa mặt phẳng bờ \({d_1}:x = 3\) chứa điểm \(O\left( {0;0} \right).\)
Xác định miền nghiệm của bất phương trình \(x \ge - 1\) là nửa mặt phẳng bờ \({d_3}:x = - 1\) chứa điểm \(O\left( {0;0} \right).\)
Xác định miền nghiệm của bất phương trình \(y \ge - 2\) là nửa mặt phẳng bờ \({d_4}:y = - 2\) chứa điểm \(O\left( {0;0} \right).\)
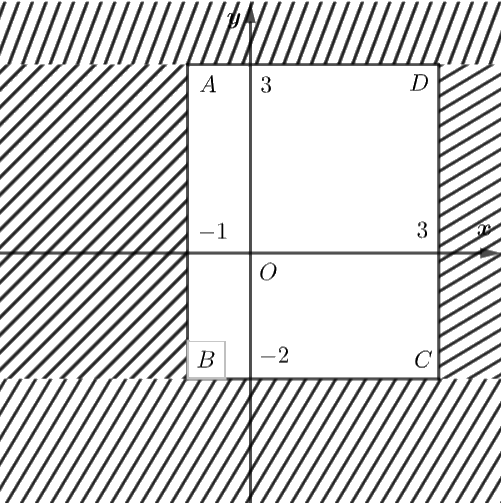
Miền nghiệm của hệ bất phương trình trên là: hình chữ nhật \(ABCD\) với \(A\left( { - 1;3} \right),\,\,B\left( { - 1; - 2} \right),\,\,C\left( {3; - 2} \right),\,\,D\left( {3;3} \right).\)
Bài 2.6 trang 23 sách bài tập Toán 10 - Kết nối tri thức với cuộc sống là một bài toán ứng dụng thực tế, đòi hỏi học sinh phải nắm vững kiến thức về vectơ và các phép toán vectơ. Dưới đây là hướng dẫn giải chi tiết bài toán này:
Cho tam giác ABC. Gọi M là trung điểm của BC. Tìm vectơ AM theo hai vectơ AB và AC.
Để tìm vectơ AM theo hai vectơ AB và AC, ta sử dụng quy tắc trung điểm và quy tắc cộng vectơ.
vectơ AM = vectơ AB + vectơ BM
vectơ AM = vectơ AB + vectơ MC
vectơ MC = vectơ AC - vectơ AM
vectơ AM = vectơ AB + (vectơ AC - vectơ AM)
2 * vectơ AM = vectơ AB + vectơ AC
vectơ AM = (vectơ AB + vectơ AC) / 2
Vậy, vectơ AM được biểu diễn theo hai vectơ AB và AC là: vectơ AM = (vectơ AB + vectơ AC) / 2
Ngoài bài 2.6, còn rất nhiều bài tập tương tự liên quan đến vectơ và các phép toán vectơ. Để giải quyết các bài tập này, bạn cần nắm vững các kiến thức sau:
Khi gặp một bài tập mới, hãy xác định rõ các vectơ đã cho và vectơ cần tìm. Sau đó, sử dụng các quy tắc và công thức đã học để biểu diễn vectơ cần tìm theo các vectơ đã cho.
Vectơ không chỉ là một khái niệm trừu tượng trong toán học mà còn có rất nhiều ứng dụng trong thực tế, như:
Việc hiểu rõ về vectơ và các phép toán vectơ sẽ giúp bạn giải quyết các bài toán thực tế một cách hiệu quả hơn.
Để củng cố kiến thức về vectơ và các phép toán vectơ, bạn có thể luyện tập thêm các bài tập sau:
Chúc các bạn học tốt!